Как нарисовать 4 мерный куб. Для всех и обо всем. Можно ли представить четырёхмерное пространство и гиперкуб

τέσσερες ἀκτῖνες - четыре луча) - четырёхмерный гиперкуб - куб в четырёхмерном пространстве . Другие названия: 4-куб , тетракуб (от др.-греч. τέτταρες - «четыре»), восьмияче́йник , октахор (от др.-греч. οκτώ - «восемь» и χώρος - «место, пространство»), гиперкуб (если число измерений не оговаривается).

В одномерном «пространстве» - на линии - выделим отрезок АВ длиной L. На двумерной плоскости на расстоянии L от АВ нарисуем параллельный ему отрезок DC и соединим их концы. Получится квадрат CDBA. Повторив эту операцию с плоскостью, получим трёхмерный куб CDBAGHFE. А сдвинув куб в четвёртом измерении (перпендикулярно первым трём) на расстояние L, мы получим гиперкуб CDBAGHFEKLJIOPNM.

Одномерный отрезок АВ служит стороной двумерного квадрата CDBA, квадрат - стороной куба CDBAGHFE, который, в свою очередь, будет стороной четырёхмерного гиперкуба. Отрезок прямой имеет две граничные точки, квадрат - четыре вершины, куб - восемь. В четырёхмерном гиперкубе, таким образом, окажется 16 вершин: 8 вершин исходного куба и 8 сдвинутого в четвёртом измерении. Он имеет 32 ребра - по 12 дают начальное и конечное положения исходного куба, и ещё 8 рёбер «нарисуют» восемь его вершин, переместившихся в четвёртое измерение. Те же рассуждения можно проделать и для граней гиперкуба. В двумерном пространстве она одна (сам квадрат), у куба их 6 (по две грани от переместившегося квадрата и ещё четыре опишут его стороны). Четырёхмерный гиперкуб имеет 24 квадратные грани - 12 квадратов исходного куба в двух положениях и 12 квадратов от двенадцати его рёбер.

Как сторонами квадрата являются 4 одномерных отрезка, а сторонами (гранями) куба являются 6 двухмерных квадратов, так и для «четырёхмерного куба» (тессеракта) сторонами являются 8 трёхмерных кубов. Пространства противоположных пар кубов тессеракта (то есть трёхмерные пространства, которым эти кубы принадлежат) параллельны. На рисунке это кубы: CDBAGHFE и KLJIOPNM, CDBAKLJI и GHFEOPNM, EFBAMNJI и GHDCOPLK, CKIAGOME и DLJBHPNF.

Аналогичным образом можно продолжить рассуждения для гиперкубов большего числа измерений, но гораздо интереснее посмотреть, как для нас, жителей трёхмерного пространства, будет выглядеть четырёхмерный гиперкуб. Воспользуемся для этого уже знакомым методом аналогий.

Возьмём проволочный куб ABCDHEFG и поглядим на него одним глазом со стороны грани. Мы увидим и можем нарисовать на плоскости два квадрата (ближнюю и дальнюю его грани), соединённые четырьмя линиями - боковыми рёбрами. Аналогичным образом четырёхмерный гиперкуб в пространстве трёх измерений будет выглядеть как два кубических «ящика», вставленных друг в друга и соединённых восемью рёбрами. При этом сами «ящики» - трёхмерные грани - будут проецироваться на «наше» пространство, а линии, их соединяющие, протянутся в направлении четвёртой оси. Можно попытаться также представить себе куб не в проекции, а в пространственном изображении.

Подобно тому, как трёхмерный куб образуется квадратом, сдвинутым на длину грани, куб, сдвинутый в четвёртое измерение, сформирует гиперкуб. Его ограничивают восемь кубов, которые в перспективе будут выглядеть как некая довольно сложная фигура. Сам же четырёхмерный гиперкуб состоит из бесконечного количества кубов, подобно тому как трёхмерный куб можно «нарезать» на бесконечное количество плоских квадратов.

Разрезав шесть граней трёхмерного куба, можно разложить его в плоскую фигуру - развёртку . Она будет иметь по квадрату с каждой стороны исходной грани плюс ещё один - грань, ей противоположную. А трёхмерная развёртка четырёхмерного гиперкуба будет состоять из исходного куба, шести кубов, «вырастающих» из него, плюс ещё одного - конечной «гиперграни».

Свойства тессеракта представляют собой продолжение свойств геометрических фигур меньшей размерности в четырёхмерное пространство.

Развёртки тессеракта

Аналогично тому, как поверхность куба может быть развёрнута в многоугольник, состоящий из шести квадратов , поверхность тессеракта может быть развёрнута в трёхмерное тело, состоящее из восьми кубов .

Существует 261 развёртка тессеракта . Развёртки гиперкуба могут быть найдены перечислением «сдвоенных деревьев», где «сдвоенное дерево» (paired tree ) - это дерево с чётным числом вершин, которые разбиты на пары так, что ни одна пара не состоит из двух смежных вершин. Между «сдвоенными деревьями» с 8 вершинами и развёртками тессеракта существует взаимно однозначное соответствие . Всего существует 23 дерева с 8 вершинами, при разбиении вершин которых на пары несмежных вершин получается 261 «сдвоенное дерево» с 8 вершинами .

Крестообразная развёртка тессеракта является элементом картины Сальвадора Дали «Corpus Hypercubus » (1954) .

Проекции

На двумерное пространство

Данная структура сложна для воображения, но возможно спроектировать тессеракт в двумерные или трёхмерные пространства . Кроме того, проецирование на плоскость позволяет легко понять расположение вершин гиперкуба. Таким образом, можно получить изображения, которые больше не отражают пространственные отношения в пределах тессеракта, но которые иллюстрируют структуру связи вершин, как в следующих примерах:

На трёхмерное пространство

Одна из проекций тессеракта на трёхмерное пространство представляет собой два вложенных трёхмерных куба, соответствующие вершины которых соединены между собой отрезками. Внутренний и внешний кубы имеют разные размеры в трёхмерном пространстве, но в четырёхмерном пространстве это равные кубы. Для понимания равности всех кубов тессеракта была создана вращающаяся модель тессеракта.

Шесть усечённых пирамид по краям тессеракта - это изображения равных шести кубов. Однако эти кубы для тессеракта - как квадраты (грани) для куба. Но на самом деле тессеракт можно разделить на бесконечное количество кубов, как куб - на бесконечное количество квадратов, или квадрат - на бесконечное число отрезков.

Ещё одна интересная проекция тессеракта на трёхмерное пространство представляет собой ромбододекаэдр с проведёнными четырьмя его диагоналями, соединяющими пары противоположных вершин при больших углах ромбов. При этом 14 из 16 вершин тессеракта проецируются в 14 вершин ромбододекаэдра , а проекции 2 оставшихся совпадают в его центре. В такой проекции на трёхмерное пространство сохраняются равенство и параллельность всех одномерных, двухмерных и трёхмерных сторон.

Стереопара

Стереопара тессеракта изображается как две проекции на плоскость одного из вариантов трёхмерного представления тессеракта. Стереопара рассматривается так, чтобы каждый глаз видел только одно из этих изображений, возникает стереоскопический эффект, позволяющий лучше воспринять проекцию тессеракта на трёхмерное пространство.

Тессеракт в культуре

В одном эпизоде «Приключений Джимми Нейтрона» «мальчик-гений» Джимми изобретает четырёхмерный гиперкуб, идентичный фолдбоксу из романа «Дорога славы » (1963) Роберта Хайнлайна .
В романе «Дорога славы » Хайнлайна описана гиперразмерная шкатулка, которая была изнутри больше, чем снаружи.
В рассказе «…И построил он себе скрюченный домишко» (в другом варианте перевода «Дом, который построил Тил») Хайнлайна описан восьмиквартирный дом в форме развёрнутого тессеракта.
Рассказ Генри Каттнера «Все тенали бороговы» описывает развивающую игрушку для детей из далёкого будущего, по строению похожую на тессеракт.
В романе Алекса Гарленда «Тессеракт» 1999 года, термин «тессеракт» используется для трёхмерной развёртки четырёхмерного гиперкуба, а не гиперкуба непосредственно. Это метафора, призванная показать, что познающая система должна быть шире познаваемой.
Сюжет фильма «Куб 2: Гиперкуб » сосредотачивается на восьми незнакомцах, пойманных в ловушку в «гиперкубе», или сети связанных трёхмерных проекций одного «гиперкуба».
В серии фильмов «Кинематографическая вселенная Marvel » Тессеракт - это ключевой элемент сюжета, космический артефакт в форме гиперкуба.
Сюжет фильма «Мстители » сосредоточен на использовании куба «Тессеракт» как неиссякаемого источника космической энергии, для открытия портала в другое «измерение» с целью осуществления плана по захвату мира (в обмен на Тессеракт - читаури предоставят Локи армию для захвата Земли). Однако этот материал не имеет почти ничего общего с общей теории четырех измерений.
В комиксе «Дэдпул уничтожает Вселенную Marvel» главный герой при помощи суперзлодея Аркады использует тессеракт, чтобы поймать Китти Прайд: её способности не смогли ей помочь выйти из куба.
Телесериал «

Бакаляр Мария

Изучаются способы введения понятия четырёхмерного куба (тессеракта), его строение и некоторые свойства Решается вопрос о том, какие трёхмерные объекты получаются при пересечении четырёхмерного куба гиперплоскостями, параллельными его трёхмерным граням, а также гиперплоскостями, перпендикулярными его главной диагонали. Рассмотрен применяемый для исследования аппарат многомерной аналитической геометрии.

Скачать:

Предварительный просмотр:

Введение……………………………………………………………………….2

Основная часть………………………………………………………………..4

Выводы………….. …………………………………………………………..12

Список литературы…………………………………………………………..13

Введение

Четырёхмерное пространство издавна привлекало внимание, как профессиональных математиков, так и людей, далёких от занятий этой наукой. Интерес к четвёртому измерению может быть обусловлен предположением о том, что наш трёхмерный мир «погружен» в четырёхмерное пространство подобно тому, как плоскость «погружена» в трёхмерное пространство, прямая «погружена» в плоскость, а точка – в прямую. Помимо этого, четырёхмерное пространство играет важную роль в современной теории относительности (так называемое пространство-время или пространство Минковского), а также может рассматриваться как частный случай мерного евклидова пространства (при ).

Четырёхмерный куб (тессеракт) является объектом четырёхмерного пространства, имеющим максимально возможную размерность (подобно тому, как обычный куб является объектом трёхмерного пространства). Заметим, что он представляет и непосредственный интерес, а именно может фигурировать в оптимизационных задачах линейного программирования (как область, в которой отыскивается минимум или максимум линейной функции четырёх переменных), а также применяется в цифровой микроэлектронике (при программировании работы дисплея электронных часов). Кроме этого, сам процесс изучения четырёхмерного куба способствует развитию пространственного мышления и воображения.

Следовательно, изучение строения и специфических свойств четырёхмерного куба является достаточно актуальным. Стоит отметить, что в плане строения четырёхмерный куб изучен достаточно хорошо. Гораздо больший интерес представляет характер его сечений различными гиперплоскостями. Таким образом, основной целью данной работы является изучение строения тессеракта, а также выяснение вопроса о том, какие трёхмерные объекты будут получаться, если четырёхмерный куб рассекать гиперплоскостями, параллельными какой-то одной из его трёхмерных граней, или же гиперплоскостями, перпендикулярными его главной диагонали. Гиперплоскостью в четырёхмерном пространстве будем называть трёхмерное подпространство. Можно сказать, что прямая на плоскости – одномерная гиперплоскость, плоскость в трёхмерном пространстве – двумерная гиперплоскость.

Поставленная цель определила задачи исследования:

1) Изучить основные факты многомерной аналитической геометрии;

2) Изучить особенности построения кубов размерностей от 0 до 3;

3) Изучить строение четырёхмерного куба;

4) Аналитически и геометрически описать четырёхмерный куб;

5) Изготовить модели развёрток и центральных проекций трёхмерного и четырёхмерного кубов.

6) Пользуясь аппаратом многомерной аналитической геометрии, описать трёхмерные объекты, получающиеся при пересечении четырёхмерного куба гиперплоскостями, параллельными какой-то одной из его трёхмерных граней, или же гиперплоскостями, перпендикулярными его главной диагонали.

Полученная таким образом информация позволит лучше разобраться в строении тессеракта, а также выявить глубокую аналогию в строении и свойствах кубов различных размерностей.

Основная часть

Сначала опишем математический аппарат, которым мы будем пользоваться в ходе данного исследования.

1) Координаты вектора: если , то

2) Уравнение гиперплоскости с нормальным вектором имеет вид Здесь

3) Плоскости и параллельны тогда и только тогда, когда

4) Расстояние между двумя точками определяется следующим образом: если , то

5) Условие ортогональности векторов:

Прежде всего, выясним, каким образом можно описать четырёхмерный куб. Сделать это можно двумя способами – геометрическим и аналитическим.

Если говорить о геометрическом способе задания, то здесь целесообразно проследить процесс построения кубов, начиная с нулевой размерности. Куб нулевой размерности – это точка (заметим, кстати, что точка может также играть роль шара нулевой размерности). Далее введём первое измерение (ось абсцисс) и на соответствующей оси отметим две точки (два нульмерных куба), находящиеся на расстоянии 1 друг от друга. Получится отрезок - одномерный куб. Сразу же отметим характерную особенность: Границей (концами) одномерного куба (отрезка) являются два нульмерных куба (две точки). Далее введём второе измерение (ось ординат) и на плоскости построим два одномерных куба (два отрезка), концы которых находятся на расстоянии 1 друг от друга (фактически, один из отрезков является ортогональной проекцией другого). Соединяя соответствующие концы отрезков, получим квадрат – двумерный куб. Опять-таки отметим, что границей двумерного куба (квадрата) являются четыре одномерных куба (четыре отрезка). Наконец, введём третье измерение (ось аппликат) и построим в пространстве два квадрата таким образом, чтобы один из них являлся ортогональной проекцией другого (при этом соответствующие вершины квадратов находятся друг от друга на расстоянии 1). Соединим соответствующие вершины отрезками – получим трёхмерный куб. Видим, что границей трёхмерного куба являются шесть двумерных кубов (шесть квадратов). Описанные построения позволяют выявить следующую закономерность: на каждом шаге мерный куб «движется, оставляя след» в е измерение на расстояние 1, при этом, направление движения перпендикулярно кубу. Именно формальное продолжение этого процесса и позволяет прийти к понятию четырёхмерного куба. А именно, заставим трёхмерный куб продвинуться в направлении четвёртого измерения (перпендикулярно кубу) на расстояние 1. Действуя аналогично предыдущему, то есть, соединяя соответствующие вершины кубов, мы и получим четырёхмерный куб. необходимо отметить, что геометрически такое построение в нашем пространстве невозможно (ибо оно трёхмерно), однако здесь мы не сталкиваемся ни с какими противоречиями с логической точки зрения. Теперь перейдём к аналитическому описанию четырёхмерного куба. Оно также получается формально, с помощью аналогии. Итак, аналитическое задание нульмерного единичного куба имеет вид:

Аналитическое задание одномерного единичного куба имеет вид:

Аналитическое задание двумерного единичного куба имеет вид:

Аналитическое задание трёхмерного единичного куба имеет вид:

Теперь уже очень легко дать аналитическое представление четырёхмерного куба, а именно:

Как видим, и при геометрическом, и при аналитическом способах задания четырёхмерного куба использовался метод аналогий.

Теперь, используя аппарат аналитической геометрии, выясним, какое имеет строение четырёхмерный куб. Сначала выясним, какие элементы в него входят. Здесь опять можно воспользоваться аналогией (для выдвижения гипотезы). Границей одномерного куба являются точки (нульмерные кубы), двумерного куба – отрезки (одномерные кубы), трёхмерного куба – квадраты (двумерные грани). Можно предположить, что границей тессеракта являются трёхмерные кубы. Для того чтобы это доказать, уточним, что понимается под вершинами, рёбрами и гранями. Вершинами куба назовём его угловые точки. То есть, координатами вершин могут являться нули или единицы. Таким образом, обнаруживается связь между размерностью куба и числом его вершин. Применим комбинаторное правило произведения – так как вершина мерного куба имеет ровно координат, каждая из которых равна нулю или единице (независимо от всех остальных), то всего имеется вершин. Таким образом, у любой вершины все координаты фиксированы и могут равняться или . Если же зафиксировать все координаты (положив каждую из них равной или , независимо от остальных), кроме одной, то получим прямые, содержащие рёбра куба. Аналогично предыдущему, можно сосчитать, что их ровно штук. А если теперь зафиксировать все координаты (положив каждую из них равной или , независимо от остальных), кроме каких-нибудь двух, получим плоскости, содержащие двумерные грани куба. Используя правило комбинаторики, найдём, что их ровно штук. Далее аналогично – зафиксировав все координаты (положив каждую из них равной или , независимо от остальных), кроме каких-нибудь трёх, получим гиперплоскости, содержащие трёхмерные грани куба. Пользуясь тем же правилом, вычислим их количество – ровно и т.д. Для нашего исследования этого будет достаточно. Применим полученные результаты к строению четырёхмерного куба, а именно, во всех выведенных формулах положим . Стало быть, четырёхмерный куб имеет: 16 вершин, 32 ребра, 24 двумерные грани, и 8 трёхмерных граней. Для наглядности зададим аналитически все его элементы.

Вершины четырёхмерного куба:

Рёбра четырёхмерного куба ():

Двумерные грани четырёхмерного куба (аналогичные ограничения):

Трёхмерные грани четырёхмерного куба (аналогичные ограничения):

Теперь, когда строение четырёхмерного куба и способы его задания описаны с достаточной полнотой, приступим к реализации главной цели – выяснению характера различных сечений куба. Начнём с элементарного случая, когда сечения куба параллельны одной из его трёхмерных граней. Например, рассмотрим его сечения гиперплоскостями, параллельными грани Из аналитической геометрии известно, что любое такое сечение будет задаваться уравнением Зададим соответствующие сечения аналитически:

Как видим, получено аналитическое задание трёхмерного единичного куба, лежащего в гиперплоскости

Для установления аналогии запишем сечение трёхмерного куба плоскостью Получим:

Это квадрат, лежащий в плоскости . Аналогия очевидна.

Сечения четырёхмерного куба гиперплоскостями дают совершенно аналогичные результаты. Это будут также единичные трёхмерные кубы, лежащие в гиперплоскостях соответственно.

Сейчас рассмотрим сечения четырёхмерного куба гиперплоскостями, перпендикулярными его главной диагонали. Сначала решим эту задачу для трёхмерного куба. Используя вышеописанный способ задания единичного трёхмерного куба, заключает, что в качестве главной диагонали можно взять, например, отрезок с концами и . Значит, вектор главной диагонали будет иметь координаты . Следовательно, уравнение любой плоскости, перпендикулярной главной диагонали, будет иметь вид:

Определим границы изменения параметра . Так как , то, почленно складывая эти неравенства, получим:

Или .

Если , то (в силу ограничений). Аналогично - если , то . Значит, при и при секущая плоскость и куб имеют ровно одну общую точку ( и соответственно). Теперь заметим следующее. Если (опять-таки в силу ограничений переменных). Соответствующие плоскости пересекают сразу три грани, ибо, в противном случае, секущая плоскость была бы параллельна одной из них, что не имеет места по условию. Если , то плоскость пересекает все грани куба. Если же , то плоскость пересекает грани . Приведём соответствующие выкладки.

Пусть Тогда плоскость пересекает грань по прямой , причём . Грань , причём . Грань плоскость пересекает по прямой , причём

Пусть Тогда плоскость пересекает грань:

грань по прямой , причём .

На этот раз получается шесть отрезков, имеющих последовательно общие концы:

Пусть Тогда плоскость пересекает грань по прямой , причём . Грань плоскость пересекает по прямой , причём . Грань плоскость пересекает по прямой , причём . То есть, получаются три отрезка, имеющих попарно общие концы: Таким образом, при указанных значениях параметра плоскость будет пересекать куб по правильному треугольнику с вершинами

Итак, здесь приведено исчерпывающее описание плоских фигур, получающихся при пересечении куба плоскостью, перпендикулярной его главной диагонали. Основная идея состояла в следующем. Необходимо понять, какие грани пересекает плоскость, по каким множествам она их пересекает, как эти множества связаны между собой. Например, если выяснялось, что плоскость пересекает ровно три грани по отрезкам, которые имеют попарно общие концы, то сечением являлся равносторонний треугольник (что доказывается непосредственным подсчётом длин отрезков), вершинами которого и служат эти концы отрезков.

Пользуясь этим же аппаратом и той же идеей исследования сечений, совершенно аналогично можно вывести следующие факты:

1) Вектор одной из главных диагоналей четырёхмерного единичного куба имеет координаты

2) Любая гиперплоскость, перпендикулярная главной диагонали четырёхмерного куба, может быть записана в виде .

3) В уравнении секущей гиперплоскости параметр может изменяться от 0 до 4;

4) При и секущая гиперплоскость и четырёхмерный куб имеют одну общую точку (и соответственно);

5) При в сечении будет получаться правильный тетраэдр;

6) При в сечении будет получаться октаэдр;

7) При в сечении будет получаться правильный тетраэдр.

Соответственно, здесь гиперплоскость пересекает тессеракт по плоскости, на которой в силу ограничений переменных выделяется треугольная область (аналогия – плоскость пересекала куб по прямой, на которой в силу ограничений переменных выделялся отрезок). В случае 5) гиперплоскость пересекает ровно четыре трёхмерные грани тессеракта, то есть, получаются четыре треугольника, имеющих попарно общие стороны, иначе говоря, образующие тетраэдр (как это можно подсчитать - правильный). В случае 6) гиперплоскость пересекает ровно восемь трёхмерных граней тессеракта, то есть, получаются восемь треугольников, имеющих последовательно общие стороны, иначе говоря, образующие октаэдр. Случай 7) полностью аналогичен случаю 5).

Проиллюстрируем сказанное конкретным примером. А именно, исследуем сечение четырёхмерного куба гиперплоскостью В силу ограничений переменных, данная гиперплоскость пересекает следующие трёхмерные грани: Грань пересекается по плоскости В силу ограничений переменных имеем: Получим треугольную область с вершинами Далее, получим треугольник При пересечении гиперплоскости с гранью получим треугольник При пересечении гиперплоскости с гранью получим треугольник Таким образом, вершины тетраэдра имеют следующие координаты . Как легко подсчитать, этот тетраэдр действительно является правильным.

Выводы

Итак, в процессе данного исследования были изучены основные факты многомерной аналитической геометрии, изучены особенности построения кубов размерностей от 0 до 3, изучено строение четырёхмерного куба, аналитически и геометрически описан четырёхмерный куб, изготовлены модели развёрток и центральных проекций трёхмерного и четырёхмерного кубов, аналитически описаны трёхмерные объекты, получающиеся при пересечении четырёхмерного куба гиперплоскостями, параллельными какой-то одной из его трёхмерных граней, или же гиперплоскостями, перпендикулярными его главной диагонали.

Проведённое исследование позволило выявить глубокую аналогию в строении и свойствах кубов различных размерностей. Использованную методику проведения аналогии можно применить при исследовании, например, мерной сферы или мерного симплекса. А именно, мерную сферу можно определить как множество точек мерного пространства, равноудалённых от заданной точки, которая называется центром сферы. Далее, мерный симплекс можно определить как часть мерного пространства, ограниченную минимальным числом мерных гиперплоскостей. Например, одномерный симплекс – отрезок (часть одномерного пространства, ограниченная двумя точками), двумерный симплекс – треугольник (часть двумерного пространства, ограниченная тремя прямыми), трёхмерный симплекс – тетраэдр (часть трёхмерного пространства, ограниченная четырьмя плоскостями). Наконец, мерный симплекс определим как часть мерного пространства, ограниченную гиперплоскостью размерности .

Отметим, что, несмотря на многочисленные применения тессеракта в некоторых областях науки, данное исследование всё же является в значительной степени математическим изысканием.

Список литературы

1) Бугров Я.С., Никольский С.М. Высшая математика, т.1 –М.: Дрофа, 2005 – 284 с.

2) Квант. Четырёхмерный куб / Дужин С., Рубцов В., №6, 1986.

3) Квант. Как начертить мерный куб / Демидович Н.Б., №8, 1974.

Точек (±1, ±1, ±1, ±1). Иначе говоря, он может быть представлен в виде следующего множества:

Тессеракт ограничен восемью гиперплоскостями , пересечение которых с самим тессерактом задаёт его трёхмерные грани (являющиеся обычными кубами). Каждая пара непараллельных трёхмерных граней пересекается, образуя двумерные грани (квадраты), и так далее. Окончательно, тессеракт обладает 8 трёхмерными гранями, 24 двумерными, 32 рёбрами и 16 вершинами.

Проекции

На двумерное пространство

Данная структура сложна для воображения, но возможно спроектировать тессеракт в двумерные или трёхмерные пространства . Кроме того, проектирование на плоскость позволяет легко понять расположение вершин гиперкуба. Таким образом, можно получить изображения, которые больше не отражают пространственные отношения в пределах тессеракта, но которые иллюстрируют структуру связи вершин, как в следующих примерах:

Третья картинка демонстрирует тессеракт в изометрии , относительно точки построения. Это представление представляет интерес при использовании тессеракта как основания для топологической сети, чтобы связать многократные процессоры в параллельных вычислениях.

На трёхмерное пространство

Шесть усечённых пирамид по краям тессеракта - это изображения равных шести кубов. Однако эти кубы для тессеракта - как квадраты (грани) для куба. Но на самом деле тессеракт можно разделить на бесконечное количество кубов, как куб - на бесконечное количество квадратов, или квадрат - на бесконечное число отрезков.

Стереопара

Стереопара тессеракта изображается как две проекции на трёхмерное пространство. Такое изображение тессеракта разрабатывалось с целью представить глубину, как четвёртое измерение. Стереопара рассматривается так, чтобы каждый глаз видел только одно из этих изображений, возникает стереоскопическая картина, воспроизводящая глубину тессеракта.

Развёртка тессеракта

Поверхность тессеракта может быть развёрнута в восемь кубов (аналогично тому, как поверхность куба может быть развёрнута в шесть квадратов). Существует 261 различная развёртка тессеракта . Развёртки тессеракта могут быть подсчитаны нанесением на граф соединённых углов.

Тессеракт в искусстве

У Эдвине А. «Новая Равнина Абботта», гиперкуб выступает рассказчиком.
В одном эпизоде «Приключений Джимми Нейтрона» «мальчик-гений» Джимми изобретает четырёхмерный гиперкуб, идентичный фолдбоксу из романа «Дорога славы » (1963) Роберта Хайнлайна .
Роберт Э. Хайнлайн упоминал гиперкубы, по крайней мере, в трёх научно-фантастических рассказах. В «Доме четырёх измерений» («Дом, который построил Тил», ) он описал дом, построенный как развёртка тессеракта, а затем вследствие землетрясения «сложившийся» в четвёртом измерении и ставший «реальным» тессерактом.
В романе «Дорога славы » Хайнлайна описана гиперразмерная шкатулка, которая была изнутри больше, чем снаружи.
Рассказ Генри Каттнера «Все тенали бороговы» описывает развивающую игрушку для детей из далёкого будущего, по строению похожую на тессеракт.
В романе Алекса Гарленда (), термин «тессеракт» используется для трёхмерной развёртки четырёхмерного гиперкуба, а не гиперкуба непосредственно. Это метафора, призванная показать, что познающая система должна быть шире познаваемой.
Сюжет фильма «Куб 2: Гиперкуб » сосредотачивается на восьми незнакомцах, пойманных в ловушку в «гиперкубе», или сети связанных кубов.
Телесериал «Андромеда » использует тессеракт-генераторы как устройство заговора. Они прежде всего предназначены, чтобы управлять пространством и временем .
Картина «Распятие на кресте » (Corpus Hypercubus) Сальвадора Дали ().
Комиксы «Nextwave comic book» изображают средство передвижения, включающее в себя 5 зон тессеракта.
В альбоме Voivod Nothingface одна из композиций названа «В моём гиперкубе».
В романе Энтони Пирса «Маршрут Куба» одна из орбитальных лун Международной ассоциации развития называется тессерактом, который был сжат в 3 измерения.
В сериале «Школа „Чёрная дыра“ » в третьем сезоне есть серия «Тессеракт». Лукас нажимает на секретную кнопку и школа начинает «складываться как математический тессеракт».
Термин «тессеракт» и производный от него термин «тессировать» встречается в повести Мадлен Л’Энгл «Складка времени».
TesseracT название британской джент группы.
В серии фильмов Кинематографическая вселенная Marvel Тессеракт - это ключевой элемент сюжета, космический артефакт в форме гиперкуба.
В рассказе Роберта Шекли «Мисс Мышка и четвертое измерение» один писатель-эзотерик, знакомец автора, пытается увидеть тессеракт, часами глядя на сконструированный им прибор: шар на ножке с воткнутыми в него стержнями, на которые насажены кубы, обклеенные всеми подряд эзотерическими символами. В рассказе упоминается труд Хинтона.
В фильмах Первый Мститель, Мстители. Тессеракт-энергия все вселенной

Другие названия

Гексадекахорон (англ. Hexadecachoron )
Октохорон (англ. Octachoron )
Тетракуб
4-Куб
Гиперкуб (если не оговаривается число измерений)

Примечания

Литература

Charles H. Hinton. Fourth Dimension, 1904. ISBN 0-405-07953-2
Martin Gardner, Mathmatical Carnival, 1977. ISBN 0-394-72349-X
Ian Stewart, Concepts of Modern Mathematics, 1995. ISBN 0-486-28424-7

Ссылки

На русском языке

Программа Transformator4D. Формирование моделей трёхмерных проекций четырёхмерных объектов (в том числе и Гиперкуба).
Программа, реализующая построение тессеракта и все его афинные преобразования, с исходниками на С++.

На английском языке

Mushware Limited - программа вывода тессеракта (Tesseract Trainer , лицензия совместима с GPLv2) и шутер от первого лица в четырёхмерном пространстве (Adanaxis ; графика, в основном, трёхмерная; есть версия под GPL в репозиториях ОС).

Многогранники

Правильные
(Платоновы тела)

Звёздчатый додекаэдр Звёздчатый икосододекаэдр Звёздчатый икосаэдр Звёздчатый многогранник Звёздчатый октаэдр

Выпуклые

Архимедовы тела	Кубооктаэдр Икосододекаэдр Усечённый тетраэдр Усечённый октаэдр Усечённый икосаэдр Усечённый куб Усечённый додекаэдр Ромбокубоктаэдр Ромбоикосододекаэдр Ромбоусечённый кубоктаэдр Ромбоусечённый икосододекаэдр Курносый куб Курносый додекаэдр Усечённый кубооктаэдр Усечённый икосододекаэдр Правильная призма Антипризма
Каталановы тела	Ромбододекаэдр Ромботриаконтаэдр Триакистетраэдр Тетракисгексаэдр Пентакисдодекаэдр Триакисоктаэдр Триакисикосаэдр Дельтоидальный икоситетраэдр Дельтоидальный гексеконтаэдр Пентагональный икоситетраэдр Пентагональный гексеконтаэдр Дисдакисдодекаэдр Дисдакистриаконтаэдр
Без полной пространственной симметрии	Пирамида Призма Бипирамида Антипризма Зоноэдр Параллелепипед Ромбоэдр Призматоид Усечённая пирамида
Пентагондодекаэдр Параллелоэдр

Формулы ,
теоремы ,
теории

Прочее

Wikimedia Foundation . 2010 .

Ещё когда я был студентом-первокурсником у меня с одним моим одногруппником вышел горячий спор. Он говорил, что четырёхмерный куб представить нельзя ни в каком виде, а я уверял, что его можно представить достаточно отчётливо. Тогда я даже сделал из скрепок проекцию гиперкуба на наше трёхмерное пространство… Но давайте обо всём по-порядку.

Что такое гиперкуб и четырёхмерное пространство

В нашем привычном пространстве три измерения. С геометрической точки зрения это значит, что в нём можно указать три взаимно-перпендикулярных прямых. То есть для любой прямой можно найти вторую, перпендикулярную первой, а для пары можно найти третью прямую, перпендикулярную двум первым. Найти четвёртую прямую, перпендикулярную трём имеющимся, уже не удастся.

Четырёхмерное пространство отличается от нашего только тем, что в нём есть ещё одно дополнительное направление. Если у вас уже есть три взаимно перпендикулярные прямые, то вы можете найти четвёртую, такую, что она будет перпендикуляра всем трём.

Гиперкуб это просто куб в четырёхмерном пространстве.

Можно ли представить четырёхмерное пространство и гиперкуб?

Этот вопрос сродни вопросу: «можно ли представить Тайную Вечерю, посмотрев на одноимённую картину (1495-1498) Леонардо да Винчи (1452-1519)?»

С одной стороны, вы конечно не представите то, что видел Иисус (он сидит лицом к зрителю), тем более вы не почувствуете запаха сада за окном и вкуса еды на столе, не услышите пения птиц… Вы не получите полного представления о происходившем в тот вечер, но нельзя сказать, что вы не узнаете ничего нового и что картина не представляет никакого интереса.

Аналогичная ситуация и с вопросом о гиперкубе. Полностью представить его нельзя, но можно приблизиться к пониманию, каков он.

Построение гиперкуба

0-мерный куб

Начнём с начала - с 0-мерного куба. Этот куб содержит 0 взаимно перпендикулярных граней, то есть это просто точка.

1-мерный куб

В одномерном пространстве у нас есть только одно направление. Сдвигаем точку в этом направление и получаем отрезок.

Это одномерный куб.

2-мерный куб

У нас появляется второе измерение, сдвигаем наш одномерный куб (отрезок) в направлении второго измерения и получаем квадрат.

Это куб в двумерном пространстве.

3-мерный куб

С появлением третьего измерения поступаем аналогично: сдвигаем квадрат и получаем обычный трёхмерный куб.

4-мерный куб (гиперкуб)

Теперь у нас появилось четвёртое измерение. То есть в нашем распоряжении имеется направление, перпендикулярное всем трём предыдущим. Воспользуемся им точно так же. Четырёхмерный куб будет выглядеть вот так.

Естественно, трёхмерный и четырёхмерный кубы нельзя изобразить на двумерной плоскости экрана. То, что нарисовал я - это проекции. О проекциях мы поговорим чуть позже, а пока немного голых фактов и цифр.

Количество вершин, рёбер, граней

Обратите внимание, что гранью гиперкуба является наш обычный трёхмерный куб. Если внимательно посмотреть на рисунок гиперкуба, то можно действительно найти восемь кубов.

Проекции и зрение жителя четырёхмерного пространства

Несколько слов о зрении

Мы живём в трёхмерном мире, но видим мы его двумерным. Это связано с тем, что сетчатка наших глаз расположена в плоскости, имеющей только два измерения. Именно поэтому мы способны воспринимать двумерные картины и находить их похожими на реальность.

(Конечно, благодаря аккомодации, глаз может оценить расстояние до объекта, но это уже побочное явление, связанное с оптикой, встроенной в наш глаз.)

Глаза жителя четырёхмерного пространства должны иметь трёхмерную сетчатку. Такое существо может сразу увидеть трёхмерную фигуру полностью: все её грани и внутренности. (Точно так же мы можем увидеть двумерную фигуру, все её грани и внутренности.)

Таким образом, с помощью наших органов зрения, мы не способны воспринять четырёхмерный куб так, как его воспринимал бы житель четырёхмерного пространства. Увы. Остаётся только уповать на мысленный взор и фантазию, которые, к счастью, не имеют физических ограничений.

Тем не менее, изображая гиперкуб на плоскости, я просто вынужден делать его проекцию на двумерное пространство. Учитывайте это обстоятельство, при изучении рисунков.

Пересечения рёбер

Естественно, ребра гиперкуба не пересекаются. Пересечения появляются только на рисунках. Впрочем, это не должно вызывать удивления, ведь рёбра обычного куба на рисунках тоже пересекаются.

Длины рёбер

Стоит отметить, что все грани и рёбра четырёхмерного куба равны. На рисунке они получаются не равными только потому, что расположены под разными углами к направлению взгляда. Однако можно развернуть гиперкуб так, что все проекции будут иметь одинаковую длину.

Кстати, на этом рисунке отчётливо видны восемь кубов, являющихся гранями гиперкуба.

Гиперкуб внутри пустой

В это трудно поверить, но между кубами, ограничивающими гиперкуб, заключено некоторое пространство (фрагмент четырёхмерного пространства).

Чтобы это лучше понять, давайте рассмотрим двумерную проекцию обычного трёхмерного куба (я специально сделал её несколько схематичной).

Можно ли по ней догадаться, что внутри куба есть некоторое пространство? Да, но только применив воображение. Глаз этого пространства не видит.

Это происходит потому, что рёбра, расположенные в третьем измерении (которое нельзя изобразить на плоском рисунке), теперь превратились в отрезки, лежащие в плоскости рисунка. Они больше не обеспечивают объём.

Квадраты, ограничивающие пространство куба, наложились друг на друга. Но можно представить, что в исходной фигуре (трёхмерном кубе) эти квадраты располагались в разных плоскостях, а не один поверх другого в одной плоскости, как это получилось на рисунке.

Точно так же дело обстоит и с гиперкубом. Кубы-грани гиперкуба на самом деле не накладываются, как это кажется нам на проекции, а располагаются в четырёхмерном пространстве.

Развёртки

Итак, житель четырёхмерного пространства может увидеть трёхмерный объект одновременно со всех сторон. Можем ли мы одновременно со всех сторон увидеть трёхмерный куб? Глазом - нет. Но люди придумали способ, как изобразить на плоском рисунке все грани трёхмерного куба одновременно. Такое изображение называется развёрткой.

Развёртка трёхмерного куба

Как образуется развёртка трёхмерного куба все наверно знают. Этот процесс показан на анимации.

Для наглядности края граней куба сделаны полупрозрачными.

Следует отметить, что мы способны воспринять эту двумерную картинку только благодаря воображению. Если рассмотреть фазы разворачивания с чисто двумерной точки зрения, то процесс будет казаться странным и совсем не наглядным.

Он выглядит, как постепенное появление сперва очертаний искажённых квадратов, а потом их расползание на свои места с одновременным принятием необходимой формы.

Если смотреть на разворачивающийся куб в направлении одной из его граней (с этой точки зрения куб выглядит как квадрат), то процесс образования развёртки ещё менее нагляден. Всё выглядит как выползание квадратов из начального квадрата (не развёрнутого куба).

Но не наглядна развёртка только для глаз .

Как понять 4-х мерное пространство?

Как раз благодаря воображению из неё можно почерпнуть много информации.

Развёртка четырёхмерного куба

Сделать анимированный процесс разворачивания гиперкуба хоть сколько нибудь наглядным просто невозможно. Но этот процесс можно представить. (Для этого надо посмотреть на него глазами четырёхмерного существа.)

Развёртка выглядит так.

Здесь видны все восемь кубов, ограничивающих гиперкуб.

Одинаковыми цветами покрашены грани, которые должны совместиться при сворачивании. Серыми оставлены грани для которых парных не видно. После свёртки самая верхняя грань верхнего куба должна совместиться с нижней гранью нижнего куба. (Аналогично сворачивается развёртка трёхмерного куба.)

Обратите внимание, что после свёртки все грани восьми кубиков придут в соприкосновение, замкнув гиперкуб. И наконец, представляя процесс свёртывания, не забывайте, что при свёртывании происходит не наложение кубов, а оборачивание ими некой (гиперкубической) четырёхмерной области.

Сальвадор Дали (1904-1989) много раз изображал распятие, а кресты фигурируют в очень многих его картинах. На картине «Распятие» (1954) используется развёртка гиперкуба.

Пространство-время и евклидово четырёхмерное пространство

Надеюсь, что вам удалось представить гиперкуб. Но удалось ли вам приблизиться к пониманию, как устроено четырёхмерное пространство-время в котором мы живём? Увы, не совсем.

Здесь мы говорили об евклидовом четырёхмерном пространстве, но пространство-время обладает совсем другими свойствами. В частности, при любых поворотах отрезки остаются всегда наклонены к оси времени либо под углом меньше 45 градусов, либо под углом больше 45 градусов.

Свойствам пространства времени я посвятил серию заметок.

Трехмерность изображения

Мир трехмерен. Его изображение двухмерно. Важной задачей живописи и, теперь, фотографии является передача трехмерности пространства. Некоторыми приемами владели уже римляне, потом они были забыты и начали возвращаться в классическую живопись с Ренессансом.

Основной прием создания трехмерного пространства в живописи — перспектива. Железнодорожные рельсы, удаляясь от зрителя, визуально сужаются. В живописи рельсы можно физически сузить. В фотографии перспектива возникает автоматически: камера снимет рельсы такими же зауженными, как их видит глаз. Однако не допускайте почти смыкания: оно будет выглядеть уже не перспективой, а странной фигурой; между рельсами, сторонами улицы, берегами реки должен сохраняться заметный просвет.

Важно понимать, что линейная перспектива — наиболее примитивный, реалистичный способ передачи мира.

Не случайно ее появление связано с театральными декорациями (Флоренский, “Обратная перспектива”). Условность, простота передачи театральной сцены небольшой глубины очень подходит для фотографии, лишенной разнообразия приемов, доступных в живописи.

Существуют перспективы, значительно более интересные, чем линейная. В работах китайских мастеров присутствует плавающая перспектива, когда объекты изображены одновременно снизу, сверху и спереди. Она не была технической ошибкой некомпетентных художников: легендарный автор этой техники, Guo Xi писал, что такое отображение позволяет осознать мир в его тотальности. Аналогична техника русской иконописи, в которой зритель может видеть лицо и спину персонажа одновременно. Интересным приемом иконописи, встречающимся также у западноевропейских художников, была обратная перспектива, в которой удаленные объекты, наоборот, крупнее близких, подчеркивая важность. Только в наши дни было установлено, что такая перспектива правильная: в отличие от удаленных предметов, ближний план действительно воспринимается в обратной перспективе (Раушенбах). Средствами фотошопа можно добиться обратной перспективы, увеличивая объекты заднего плана. Для привыкшего к законам фотографии зрителя смотреться такое изображение будет странно.

Введение в кадр угла здания, от которого в обе стороны расходятся стены, создает подобие изометрической перспективы. Мозг понимает, что стены находятся под прямым углом, и раскладывает остальное изображение соответственно. Такая перспектива динамичнее фронтальной и естественнее для ближнего плана. Просто вводите в кадр торцевые углы предметов и близко расположенных зданий.

За счет расширения, изометрическая перспектива мажорна, что редко подходит для классического портрета. Линейная перспектива, за счет сужения, лучше передает минорные эмоции.

На этапе съемки, фотографу доступен ряд инструментов, подчеркивающих перспективу. Уходящие вдаль объекты равной ширины (колея, улица, колонны, борозды) своим сужением и даже просто удалением обозначают зрителю трехмерность пространства. Эффект сильнее, если снимать с низкого ракурса, чтобы увеличить искажения перспективы. Для пейзажной съемки этого достаточно, но при небольшой глубине изображения интерьерной съемки эффект малозаметен. Его можно немного усилить в пост-обработке, заузив верхнюю часть изображения (Transform Perspective). Впрочем, и в пейзаже гипертрофированная перспектива может выглядеть интересно.

Глубина может быть явной по смыслу изображения: здания разделены улицей или рекой. Диагональ подчеркивает трехмерность; например, мост через реку.

Предметы известного зрителю размера на заднем плане задают масштаб и, соответственно, формируют перспективу. В пейзажной съемке таким предметом может быть автомобиль, а в портретной попробуйте присогнуть и поджать под стул ногу (от камеры), чтобы она, оставаясь видимой, казалась меньше. Можно даже чуть уменьшить эту ногу в пост-обработке.

Орнамент передает перспективу за счет визуального уменьшения элементов. Примером будет крупная плитка на полу, линии разметки на дороге.

Существует техника гипертрофированного переднего плана. Диспропорционально большой, он создает глубину изображения. Сравнивая масштаб переднего плана и модели, глаз приходит к выводу, что модель гораздо дальше, чем кажется. Гипертрофированность должна оставаться едва различимой, чтобы изображение не воспринималось ошибкой. Этот прием подходит не только для пост-обработки, но и при съемке: исказите пропорции, снимая объективом 35 или 50мм. Съемка широкоугольным объективом растягивает пространство, усиливая его трехмерность за счет нарушения пропорций. Эффект сильнее, если снимать модель с близкого расстояния, но опасайтесь гротескных пропорций: только авторы религиозных изображений могут изображать человека больше здания.

Отлично работает пересечение. Если яблоко частично закрывает собой грушу, то мозг не ошибется: яблоко находится впереди груши. Модель, частично закрывающая собой мебель, создает тем самым глубину интерьера.

Глубину изображению придает также чередование светлых и темных пятен. Мозг знает по опыту, что находящиеся рядом предметы освещены примерно одинаково, поэтому интерпретирует по-разному освещенные предметы как расположенные на разном расстоянии. Для такого эффекта, пятна чередуются в направлении оси перспективы — вглубь изображения, а не поперек него. Например, снимая модель, лежащую от камеры в темном кадре, положите блики света возле ягодиц и возле ног. Можно осветлять/ затемнять области в пост-обработке.

Последовательность все более темных предметов воспринимается уменьшающейся. За счет постепенного затенения объектов, расположенных по активной линии, можно получить тонкое ощущение перспективы. Аналогично, глубина передается ослаблением света: пустите полосу света по мебели или на полу.

Трехмерное изображение можно получить за счет не только светового, но и цветового контраста. Этот прием был известен фламандским живописцам, которые располагали на своих натюрмортах яркие цветные пятна. Красный гранат и желтый лимон рядом будут смотреться трехмерно даже при плоском фронтальном освещении. Особенно хорошо они будут выступать вперед на фоне фиолетового винограда: теплый цвет на фоне холодного. Яркие цветные поверхности хорошо вырываются из темноты даже слабым светом, типичным для натюрморта. Контраст цветов лучше работает с основными цветами: красным, желтым, синим, а не оттенками.

На черном фоне, желтый цвет выступает вперед, синий прячется назад. На белом фоне — наоборот. Насыщенность цвета усиливает этот эффект. Почему так происходит? Желтый цвет не бывает темным, поэтому мозг отказывается верить в то, что желтый предмет может быть погружен в темный фон, не освещен. Синий цвет, наоборот, темный.

Усиление перспективы в пост-обработке сводится к имитации атмосферного восприятия: удаленные объекты кажутся нам более светлыми, размытыми, со сниженным контрастом по яркости, насыщенности и тону.

Помимо больших расстояний, атмосферные эффекты естественно выглядят в утренней дымке, тумане, накуренном баре. Учитывайте погоду: в облачный день или в сумерках не может быть значительного отличия между передним и задним планами.

Самый сильный из факторов — контраст по яркости. В настройках это обычный контраст. Снизьте контрастность удаленных предметов, поднимите контрастность переднего плана — и изображение станет выпуклым. Речь не о контрасте между передним и задним планами, а о контрастности заднего плана, которая должна быть ниже контрастности переднего. Этот метод подходит не только для пейзажей и жанровой съемки, но и студийного портрета: поднимите контраст передней части лица, снизьте контраст на волосах и скулах, одежде. Портретные фильтры делают нечто похожее, размывая кожу модели и оставляя резкими глаза и губы.

Корректировка контраста — самый простой способ трехмерной пост-обработки изображения. В отличие от других процессов, зритель практически не заметит изменений, что позволит сохранить максимальную естественность.

На снижение контраста похоже размытие, но это разные процессы. Изображение может быть низкоконтрастным, оставаясь резким. В силу ограниченной глубины резкости, размытие удаленных предметов остается наиболее популярным способом передачи трехмерности на фотографии, и его легко усилить, размыв дальний план в пост-обработке. Поэтому же на заднем плане следует располагать поменьше деталей — мозг не ожидает различимых предметов вдалеке. Между тем, снижение контраста лучше отвечает естественному восприятию: удаленные горы видны низкоконтрастными, а не размытыми, потому что сканируя пейзаж, взгляд постоянно перефокусируется, ему чужда проблема глубины резкости. Размывая задний план, можно заодно поднять резкость переднего. Дополнительно, на переднем плане можно усилить линии изображения (High Pass Filter или Clarity). Именно высокая резкость переднего плана объясняет характерную выпуклость изображения высококачественных объективов. Осторожно: ради незначительного увеличения трехмерности вы можете сделать изображение слишком жестким.

Более светлые объекты кажутся более удаленными. Связано это с тем, что в природе мы видим дальние объекты сквозь толщу рассеивающего свет воздуха; дальние горы кажутся светлыми. В пейзажной съемке следует, поэтому, с осторожностью относиться к расположению светлых объектов на переднем плане.

Осветлите дальние объекты. Чем удаленнее, тем больше они сливаются с яркостью и тоном неба. Обратите внимание, что горизонтальные объекты (земля, море) лучше освещаются, чем вертикальные (стены, деревья), поэтому не переусердствуйте с осветлением последних. В любом случае, объекты должны оставаться заметно менее светлыми, чем небо.

Хорошо, если вы заметили, что осветление — это другой способ снизить контраст по яркости заднего плана. Чуть затемните передний план для усиления эффекта выпуклости.

Казалось бы, в интерьере все наоборот. Если на улице глаз привык к тому, что даль светла, то в комнате свет зачастую сосредоточен на человеке, а интерьер погружен в темноту; мозг привык к освещению переднего плана, а не заднего.

На интерьерных изображениях с малой глубиной сцены, в отличие от пейзажных, освещенная модель выступает из темного фона. Но есть и противоположный фактор: 99% своей эволюции, человек наблюдал перспективу на открытой местности, и с появлением комнат мозг еще не успел перестроиться. Вермеер предпочитал светлый фон для портретов, и они у него действительно выпуклые. Освещение вертикального фона, рекомендуемое в фотографии, не только отделяет от него модель, но и за счет осветления фона придает изображению небольшую трехмерность. Здесь мы сталкиваемся с тем, что мозг анализирует расположение объектов по нескольким факторам, и они могут быть конфликтующими.

Интересно выглядит студийное освещение, в котором световые пятна лежат на удаленных от камеры зонах модели. Например, подсвечена та грудь, которая дальше от камеры.

Снизьте насыщенность цвета на удаленных объектах: из-за толщи разделяющего нас воздуха, дальние горы десатурированы почти до уровня монохрома и покрыты синей дымкой. Насыщенность переднего плана можно увеличить.

Поскольку желтый цвет светлый, а синий и красный — темные, то цветовой контраст заодно является и контрастом по яркости.

Десатурируя удаленный фон, не дайте ему пропасть из виду. Часто, напротив, нужно поднять насыщенность дальнего плана, чтобы проявить его. Это важнее трехмерности.

Много советов по трехмерности фотографии посвящено температурному контрасту. На самом деле, этот эффект очень слабый, легко перебивается контрастом по яркости. К тому же, температурный контраст назойлив, бросается в глаза.

Очень удаленные предметы кажутся более холодного цвета, потому что воздух поглощает теплый оранжевый свет. Фотографируя модель на пляже на фоне кораблей, расположенных у горизонта, в пост-обработке снизьте цветовую температуру далекого моря и судов. Модель в красном купальнике выступает из синего моря, а модель в желтом свете уличного фонаря — из синеватых сумерек.

В этом заключается раздельное тонирование: модель делаем теплее, фон — холоднее. Мозг понимает, что в одной плоскости разных цветовых температур не бывает, и воспринимает такое изображение трехмерным, на котором модель выступает из фона. Раздельное тонирование придает глубину и пейзажам: сделайте передний план теплее, задний холоднее.

Важное исключение из раздельного тонирования: на восходе и закате, удаленный фон вовсе не холодный, а теплый, с желтыми и красно-оранжевыми тонами. Очевидное решение — использовать белокожую модель в фиолетовом купальнике — не работает, потому что закатный свет наносит теплый оттенок и на тело модели.

Обобщим: для придания фотографии трехмерности на основе атмосферных эффектов, необходимо противопоставить передний и задний планы. Основное противопоставление — по обычному контрасту: передний план контрастный, задний — слабоконтрастный. Второе противопоставление — по резкости: передний план резкий, задний — размытый. Третье противопоставление — по светлости: передний план темный, задний — светлый. Четвертое противопоставление — по насыщенности: цвета переднего плана насыщены, заднего — десатурированы. Пятое противопоставление — по температуре: передний план теплый, задний — холодный.

Перечисленные факторы нередко разнонаправленны. Желтый цвет ярче синего, а светлые предметы кажутся дальше темных. Естественно было бы ожидать, что желтый цвет отступает, а синий — приближается к зрителю. На самом деле, наоборот: теплый цвет выступает из холодного фона. То есть, цвет оказывается более сильным фактором, чем яркость. Что, по размышлении, и не удивительно: желтый и красный хорошо различимы только вблизи, и зритель не ожидает их встретить на большом расстоянии.

Итог: удерживайте задний план низкоконтрастным, размытым, светлым, десатурированным, синеватым. И будьте готовы к тому, что зритель, привыкший к гипертрофированному 3D кинофильмов, сочтет созданную вами трехмерность едва заметной или отсутствующей.

В портретной съемке, лучше полагаться на проверенный эффект chiaroscuro — игру светотени на лице модели, которая сделает изображение достаточно выпуклым. В жанровой съемке, перспектива дает наиболее заметный эффект трехмерности. В натюрморте, основным фактором будет пересечение (наложение) предметов.

Не увлекайтесь перспективой; она лишь фон для фронтальной плоскости, на которой трепещет ваше изображение. В современной живописи, далекой от реализма, перспектива не в почете.

Скачать книгу целиком: pdfepubazw3mobifb2litОглавление

В геометрии гиперкуб - это n -мерная аналогия квадрата (n = 2) и куба (n = 3). Это замкнутая выпуклая фигура, состоящая из групп параллельных линий, расположенных на противоположных краях фигуры, и соединенных друг с другом под прямым углом.

Эта фигура также известная под названием тессеракт (tesseract). Тессеракт относится к кубу, как куб относится к квадрату. Более формально, тессеракт может быть описан как правильный выпуклый четырехмерный политоп (многогранник), чья граница состоит из восьми кубических ячеек.

Согласно Окфордскому словарю английского языка, слово "tesseract" было придумано в 1888 Чарльзом Говардом Хинтоном (Charles Howard Hinton) и использовано в его книге "Новая эра мысли" ("A New Era of Thought"). Слово было образовано от греческого "τεσσερες ακτινες" ("четыре луча"), имеется в виде четыре оси координат. Кроме этого, в некоторых источниках, эту же фигуру называли тетракубом (tetracube).

n -мерный гиперкуб также называется n-кубом .

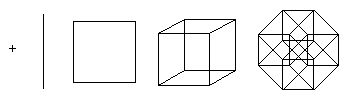
Точка - это гиперкуб размерности 0. Если сдвинуть точку на единицу длины, получится отрезок единичной длины - гиперкуб размерности 1. Далее, если сдвинуть отрезок на единицу длины в направлении перпендикулярном направлению отрезка получится куб - гиперкуб размерности 2. Сдвигая квадрат на единицу длины в направлении перпендикулярном плоскости квадрата, получается куб - гиперкуб размерности 3. Этот процесс может быть обобщен на любое количество измерений. Например, если сдвинуть куб на единицу длины в четвертом измерении, получится тессеракт.

Семейство гиперкубов является одним из немногих правильных многогранников, которые могут быть представлены в любом измерении.

Элементы гиперкуба

Гиперкуб размерности n имеет 2n "сторон" (одномерная линия имеет 2 точки; двухмерный квадрат - 4 стороны; трехмерный куб - 6 граней; четырехмерный тессеракт - 8 ячеек). Количество вершин (точек) гиперкуба равно 2 n (например, для куба - 2 3 вершин).

Количество m -мерных гиперкубов на границе n -куба равно

Например, на границе гиперкуба находятся 8 кубов, 24 квадрата, 32 ребра и 16 вершин.

Элементы гиперкубов

n-куб	Название	Вершина (0-грань)	Ребро (1-грань)	Грань (2-грань)	Ячейка (3-грань)	(4-грань)	(5-грань)	(6-грань)	(7-грань)	(8-грань)
0-куб	Точка	1
1-куб	Отрезок	2	1
2-куб	Квадрат	4	4	1
3-куб	Куб	8	12	6	1
4-куб	Тессеракт	16	32	24	8	1
5-куб	Пентеракт	32	80	80	40	10	1
6-куб	Хексеракт	64	192	240	160	60	12	1
7-куб	Хептеракт	128	448	672	560	280	84	14	1
8-куб	Октеракт	256	1024	1792	1792	1120	448	112	16	1
9-куб	Эненеракт	512	2304	4608	5376	4032	2016	672	144	18

Проекция на плоскость

Формирование гиперкуба может быть представлено следующим способом:

Две точки A и B могут быть соединены, образуя отрезок AB.
Два параллельных отрезка AB и CD могут быть соединены, образуя квадрат ABCD.
Два параллельных квадрата ABCD и EFGH могут быть соединены, образуя куб ABCDEFGH.
Два параллельных куба ABCDEFGH и IJKLMNOP могут быть соединены, образуя гиперкуб ABCDEFGHIJKLMNOP.

Последнюю структуру нелегко представить, но возможно изобразить ее проекцию на двухмерное или трехмерное пространство. Более того, проекции на двухмерную плоскость могут быть более полезны возможностью перестановки позиций спроецированных вершин. В этом случае можно получить изображения, которые больше не отражают пространственные отношения элементов внутри тессеракта, но иллюстрируют структуру соединений вершин, как на примерах ниже.

На первой иллюстрации показано, как в принципе образуется тессеракт путем соединения двух кубов. Эта схема похожа на схему создания куба из двух квадратов. На второй схеме показано, что все ребра тессеракта имеют одинаковую длину. Эта схема также заставляют искать соединенные друг с другом кубы. На третьей схеме вершины тессеракта расположены в соответствии с расстояниями вдоль граней относительно нижней точки. Эта схема интересна тем, что она используется как базовая схема для сетевой топологии соединения процессоров при организации параллельных вычислений: расстояние между любыми двумя узлами не превышает 4 длин ребер, и существует много различных путей для уравновешивания нагрузки.

Гиперкуб в искусстве

Гиперкуб появился в научно-фантастической литературе с 1940 года, когда Роберт Хайнлайн в рассказе "Дом, который построил Тил" ("And He Built a Crooked House") описал дом, построенный по форме развертки тессеракта. В рассказе этот Далее этот дом сворачивается, превращаясь в четырехмерный тессеракт. После этого гиперкуб появляется во многих книгах и новеллах.

В фильме "Куб 2: Гиперкуб" рассказывается о восьми людях, запертых в сети гиперкубов.

На картине Сальвадора Дали "Распятие" ("Crucifixion (Corpus Hypercubus)", 1954) изображен Иисус распятый на развертке тессеракта. Эту картину можно увидеть в Музее Искусств (Metropolitan Museum of Art) в Нью-Йорке.

Заключение

Гиперкуб - одна из простейших четырехмерных объектов, на примере которого можно увидеть всю сложность и необычность четвертого измерения. И то, что выглядит невозможным в трех измерениях, возможно в четырех, например, невозможные фигур. Так, например, бруски невозможного треугольника в четырех измерениях будут соединены под прямыми углами. И эта фигура будет выглядеть так со всех точек обзора, и не будет искажаться в отличие от реализаций невозможного треугольника в трехмерном пространстве (см.