Что делать если определитель матрицы равен 0. Формулы для определителя. Метод Крамера. Применение для систем линейных уравнений
Так как для нахождения обратной матрицы важно, равен ли определитель марицы нулю или нет, то введем следующие определения.
Определение 14.9 Квадратную матрицу назовем вырожденной или особенной матрицей , если , и невырожденной или неособенной матрицей , если .
Предложение 14.21 Если обратная матрица существует, то она единственна.
Доказательство . Пусть две матрицы и являются обратными для матрицы . Тогда
Следовательно, .
Правило Крамера .
Пусть матричное уравнение AX = B
Где ; – определитель, полученный из определителя D заменой i -го столбца столбцом свободных членов матрицы B :
 |
Доказательство теоремы разобъем на три части:
1.Решение системы (1) существует и является единственным.
2.Равенства (2) являются следствием матричного уравнения (1).
3.Равенства (2) влекут за собой матричное уравнение (1).
Так как , то существует и при том единственная, обратная матрица .
Умножая обе части матричного уравнения (1) слева на , получаем решение этого уравнения:
Единственность обратной матрицы доказывает первую часть теоремы.
Перейдем к доказательству взаимно-однознаяного соответствия между формулами (1) и (2).
Используя формулу (4), получим выражение для i -го элемента. Для этого нужно умножить i -ую строку матрицы
![]()
на столбец B .
Учитывая, что i -ая строка присоединенной матрицы составлена из алгебраических дополнений , получаем следующий результат:
Вывод формул Крамера завершен. Покажем теперь, что выражения
Изменим порядок суммирования в правой части полученного выражения:
где – дельта символ Кронекера.
Учитывая, что дельта символ снимает суммирование по одному из индексов, получаем требуемый результат:
Комплексные числа : Идея – определение новых объектов с помощью известных. Вещественные числа расположены на прямой. При переходе на плоскость получаем комплексные числа. Определение : Комплексным числом называется пара вещественных чисел z = (a,b). Число a = Re z называется вещественной частью, а b = Im z мнимой частью комплексного числа z .
Операции над комплексными числами: Комплексные числа z1 z2 равны Z1 = z2 ⇔ Re z1 = Re z2 & Im z1 = Im z2. Сложение: Z=z1+z2. ⇔Re z=Re z1+Re z2 & Im z1+ Im z2. Число (0,0) обозначается через 0. Это нейтральный элемент. Проверяется, что сложение комплексных чисел обладает свойствами аналогичными свойствам сложения вещественных чисел. (1. Z1+ z2 = z2 + z1 – коммутативность; 2. Z1 + (z2 + z3) = (z1 + z2) + z3 – ассоциативность; 3. Z1 + 0 = z1 - существование нуля (нейтрального элемента) ;4. z + (−z) = 0 - существование противоположного элемента). Умножение : z= z1 z2⇔Re z=Re z1 Re z2-Im z1 Im z2 & Im z1=Im z1 Re z2+Im z2 Re z1. Комплексное число z лежит на вещественной оси, если Imz = 0 . Результаты операций над такими числами совпадают с результатами операций над обычными вещественными числами. Умножение комплексных чисел обладает свойствами замкнутости, коммутативности и ассоциативности. Число (1,0) обозначается через 1. Оно является нейтральным элементом по умножению.Если a∈ R, z ∈C , то Re(az) = aRe z, Im(az) = a Imz . Определение Число (0,1) обозначается через i и называется мнимой единицей. В этих обозначениях получаем запись комплексного числа в алгебраической форме: z = a + ib, a,b∈ R. i=-1. (a,b)=(a,0)+(0,b) ;(a,0)+b(0,1)=a+ib=z; (a1+ib)(a2+ib2)=a1a2+i(a1b2+1-a2b1)-b1b2; (a+ib)(1+0i)=a+ib; z(a,b), z(0+i0)=0; z!=0; a 2 +b 2 >0 (a+ib)(a-ib/a 2 +b 2)=1.Число называется сопряженным к z, если Re =Re z ; Im =- Im z.
= + ; = ; z =(a+ib)(a-ib)=a 2 +b 2 Модулем числа z называется вещественное число| z |= . Справедлива формула| z| 2 = z Из определения следует, что z ≠ 0⇔| z|≠ 0. z -1 = /|z| 2 (1)
Тригонометрическая форма комплексного числа: a=r cos(t); b=r sin(t). Z=a+ib=r(cos(t)+isin(t)) (2) t-аргумент комплексного числа. Z1=z2 =>|z1|=|z2|
arg(z1)-arg(z2)=2пk.
Z1=r1(cos(t1)+isin(t1), Z2=r2(cos(t2)+isin(t2)), Z3=z1 z2=T1T2(cos(t1+t2)+isin(t1+t2)(1)
Arg(z1z2)=arg(z1)+arg(z2) (2)
Z!=0 z -1 = /|z| 2 =1/r(cos(-t)+i(sin(-t)) Z=r(cos(t)+istn(t))
R(cos(t)-isin(t))
Определение: Корнем степени n из единицы называются решения уравнения z n =1Предложение. Имеется n различных корней степени n из единицы. Они записываются в виде z = cos(2 π k / n) + isin(2 π k / n), k = 0,..., n −1 .Теорема. В множестве комплексных чисел уравнение всегда имеет n решений.Z=r(cos(t)+isin(t)); z n =r n (cos(nt)+isin(nt))=1(cos(0)+isin(0))=>z n =1 .Z-целые числа. K пренадлежит Z. k=2=E 2 =E n-1 E n ; E n =1; E n+p =E p . Таким образом доказано, что решениями уравнения являются вершины правильного n-угольника, причем одна из вершин совпадает с 1.
Корень n-ой степени из z 0 . Z k =Z 0 ; Z 0 =0=>Z=0; Z 0 !=0;Z=r(cos(t)-isin(t)); Z 0 =r 0 (cos(t0)+isin(t0)); r0!=0; Z n =r n (cos(nt)+isin(nt))
r n =r 0, nt-t 0 =2пk; r= ; t=(2пk+t0)/n; z= (cos((2пk+t0)/n)+isin((2пk+t0)/n)= (cos t0/n+isin t0/n)(cos(2пk/n)+isin(2пk/n))=Z 1 E k ; z=z 1 E k ; Z 1 n =z 0, k=0, n=1
Матрицы. Определение: Матрицей размера m × n называется прямоугольная таблица, содержащая m строк и n столбцов, элементы которой являются вещественными или комплексными числами. Элементы матрицы имеют двойные индексы.
Если m = n , то это квадратная матрица порядка m , а элементы с одинаковыми индексами образуют главную диагональ матрицы.
Операции над матрицами: Определение: Две матрицы A,B называются
равными, если их размеры совпадают и A = B,1≤ i ≤ m,1≤ j ≤ n
Сложение. Рассматриваются матрицы одного размера. Определение :C = A + B ⇔ C = A + B, ∀i, j Предложение . Сложение матриц коммутативно, ассоциативно, существует нейтральный элемент и для каждой матрицы существует противоположный элемент.
Нейтральным элементом является нулевая матрица, все элементы которой равны 0. Она обозначается через Θ.
Умножение. Матрица A размера m × n обозначается через Amn. Определение: С mk =A mn B nk ó
C= Заметим, что в общем случае умножение не является коммутативным. Замкнутость справедлива для квадратной матрицы фиксированного размера. Пусть даны три матрицы Amn , Bnk , Ckr . Тогда (AB)C = A(BC). Если произведение 3 матриц существует, то оно является ассоциативным.
Символ Кронекера δij . Он равен 1, если индексы совпадают, и 0 иначе. Определение. Единичной матрицей I n называется квадратная матрица порядка n , для которой выполнены равенства n I n [ i | j] = δ ij Предложение. Справедливы равенства I m A mn =A mn I n =A mn
Сложение и умножение матриц связанно законами дистрибутивности. A(B+C)=AB+AC; (A+B)C=AC+BC;(A(B+C)= = = +
Транспонирование матрицы. Транспонированная матрица - это матрица, полученная из исходной путем замены строк на столбцы.
(A+B) Т =А Т +В Т
(АВ) Т =В Т А Т;(AB) Т =(AB)= = (В Т А Т)
Умножение матрицы на число. Произведение числа а на матрицу A mn называется новая матрица B=aA
1*A=A;a(A+B)=aA+aB;(a+b)A=aA+bA;
A(BC)=(aB)C=B(aC); (ab)A=a(bA)=b(aA)
Линейным пространством (L) над полем F называется множество векторов L={α,β..}
1.α+β=β+α(коммутативность) 2.α+(β+γ)= (α+β)+γ, (ab)α=a(bα)(ассоциативность) 3.α+θ=α, α∙1=α(существование нейтрального) 4.α+(-α)=θ (существование противоположного)
a(α+β)=aα+aβ, (a+b)α=aα+bα. Док-во {|(a+b)α|=|a+b||α|, |aα|=|a||α|,|bα|=|b||α|, a и b>0, |a+b|=a+b,|a|=a,|b|=b.} aα+(-a)α=θ, (a+0)α=aα
Примером линейного пространства является множество матриц фиксированного размера с операциями сложения и умножения на число.
Система линейных векторов называется линейно зависимой , если 1.a 1 ,a 2 ..a n ≠0 2. a 1 α 1 ,a 2 α 2 ..a n α n =θ Если система не является линейно зависимой, то она линейно независима. Рассмотрим 1. n=1 α 1 завис. a 1 ≠0, a 1 α 1 =θ, a 1 -1 (a 1 α 1)= a 1 -1∙ θ=θ, (a 1 -1 a 1)α 1 =1∙α 1 =α 1 ; 2. n=2 α 1 ,α 2 завис. a 1 ≠0 ,a 1 α 1 +a 2 α 2 =θ ,α 1 = -a 1 -1 a 2 α 2 =b 2 α 2; 3.n≥2 α 1 ..α n завис. a 1 ≠0, α 1 =Σ k =2 n b k α k , 1α 1 - Σ k =2 n b k α k =θ, (1,b 2 ..b n)≠0
Предложение : Система векторов, содержащая более чем 1 вектор линейно зависима ттогда какой-то вектор системы есть линейная комбинация остальных.
Если система векторов содержит линейно зависимую подсистему, то вся система линейно зависима. Док-во: {α 1 ..α n завис. Система: α 1 ..α n ;α n +1 ..α m , a 1 α 1 +..+a n α n +0α n +1 +..+0α m =θ, a 1 ..a n ,0..0≠0.} Если система содержит нул.вектор, то она линейно зависима. Теорема о линейных пространствах : {Пусть даны 2 системы векторов α 1 ..α m , β 1 ..β n . Система векторов α выражается через β, если каждый вектор α есть линейная комбинация β α i = Σ k =1 n a ik β k , (α) { (β), (β) { (γ)→ (α) { (γ)} Теорема: Даны 2 системы векторов, при этом α независимая и, (α) { (β)→m≤n Докажем, α 1 ..α m +1 β 1 ..β m (α) { (β)→(α)завис. {Докажем методом индукции. m=1: α 1 =a 11 β 1 , α 2 =a 21 β 1 . a 11 =0→ α 1 =θ. a 11 α 2 – a 21 α 1 = a 11 a 21 β 1 - a 21 a 11 β 1 =θ. α 1 = a 11 β 1 +.. a 1 n -1 β n -1 .. α n = a n 1 β 1 +.. a nn -1 β n -1 Если все коэффициенты =0 a 11 =a 12 =..=a 1 n -1 =0→ α 1 =θ→ вся система линейно зависима. a 1 n -1 ≠0 α 2 ′= α 2 –с 2 α 1 =b 21 β 1 +..+b 2 n -2 β n -2 , c 2 =a 2 n -1 / a 1 n -1 , α 3 ′= α 3 –с 3 α 1 .. α n ′= α n –с n α 1 . По пред. индукции сущ-ет ненулевой набор чисел d 2 ..d n: d 2 α 2 ′+d 3 α 3 ′+.. d n α n ′=θ , d 2 (α 2 –с 2 α 1)+d 3 (α 3 –с 3 α 1)+.. d n (α n –с n α 1)=θ , (α) { (β), m>n →(α)завис. если (α) независ. →m≤n}
МЛНП -макс.лин.незвавис.подсистемы. Пусть дана система векторов α 1 ..α n некоторой подсис. α i 1 ..α in называется МЛНП, если 1. α 1 ..α n независ.2. α i 1 ..α ir , α ij завис. Каждый вектор системы есть линейная комбинация векторов МЛНП. { α i 1 ..α ir , α ij завис. a i 1 α i 1 +.. a ir α ir +a ij α ij =θ
a i 1 ..a ir , a ij ≠0 если a ij =0 → a i 1 α i 1 +.. a ir α ir =θ a i 1 ..a ir =0 противоречие a ij ≠0 α ij = a ij -1 (-a i 1 α i 1 -.. a ir α ir) (α 1 ..α n) { (α i 1 ..α ir)
Следствие : Любые 2 МЛНП из одной системы векторов содержат одинаковое число векторов (α i 1 ..α ir) { (α j 1 ..α jk) , (α j 1 ..α jk) { (α i 1 ..α ir) k≤r, r≤k →r=k Число векторов МЛНП называется рангом исходной системы. В случае линейного пространства(система векторов состоит из всех векторов пространства) МЛНП мб конечна или бесконечна. Рассматриваем конечный случай. Число векторов(ранг)- размерность линейного пространства. МЛНП-база. Пространство направленных отрезков. Два неколлинеарных вектора составляют базу в пространстве векторов на плоскости. α 3 = α 1 ′+ α 2 ′=a 1 α 1 + a 2 α 2 . 3 вектора линейно зависимые α 3 =a 1 α 1 + a 2 α 2 . Компланарность- 3 вектора параллельны одной плоскости α 4 = α 4 ′+ α 5 ′ , α 4 ′=a 1 α 1 + a 2 α 2 , α 5 ′= a 3 α 3 , α 4 = a 1 α 1 + a 2 α 2 + a 3 α 3 . Пространство строк длины n . α= Предложение: Пространство строк длины n имеет размерность n. { ξ 1 =<1…0> ξ 2 =<0,1…0> .. ξ n =<0…1> ,a 1 ξ 1 + a 2 ξ 2 +.. a n ξ n =θ=<0,..0> → a 1 =a 2 =..a n =0 (линейная независимость) β= β= b 1 ξ 1 + b 2 ξ 2 +.. b n ξ n →пространство строк длины n имеет размерность и n.
Ранг матрицы.
Две системы векторов α и β называются эквивалентными, если каждый вектор
α{ β(выражается) и β{ α.
Предложение. Ранги эквивалентных систем совпадают.
α i 1 , α i 2 ,…, α ir – МЛНП α , β i 1 , β i 2 ,…, β ik – МЛНП β , α i 1 , α i 2 ,…, α ir < β < β i 1 , β i 2 ,…, β ik → r<=k
Поменяв местами α и β местами → r>=k >>> Значит, r=k.
Определение. Пусть дана матрица A=
Рангом матрицы А называется ранг системы векторов α1, α2,…, αm, составленных из это матрицы >>rank(A)-ранг
Из определения очевидно, что при перестановке столбцов ранг не меняется. Покажем, что при перестановке столбцов ранг так же не меняется.
А’= 
Линейно зависимы:
b 1 α 1 + b 2 α 2 +…+ b m α m =θ, b 1 а 11 +b 2 a 21 +…+b m a m 1=0, b 1 α’ 1 + b 2 α’ 2 +…+ b m α’ m , b 1 а 11 +b 2 a 21 +…+b m a m 1=0
Постановка задачи
Задание подразумевает знакомство пользователя с основными понятиями численных методов, такими как определитель и обратная матрица , и различными способами их вычислений. В данном теоретическом отчете простым и доступным языком сначала вводятся основные понятия и определения, на основании которых проводится дальнейшее исследование. Пользователь может не иметь специальных знаний в области численных методов и линейной алгебры , но с легкостью сможет воспользоваться результатами данной работы. Для наглядности приведена программа вычисления определителя матрицы несколькими методами, написанная на языке программирования C++. Программа используется как лабораторный стенд для создания иллюстраций к отчету. А также проводится исследование методов для решения систем линейных алгебраических уравнений . Доказывается бесполезность вычисления обратной матрицы, поэтому в работе приводится более оптимальные способы решения уравнений не вычисляя ее. Рассказывается почему существует такое количество различных методов вычисления определителей и обратных матриц и разбираются их недостатки. Также рассматриваются погрешности при вычислении определителя и оценивается достигнутая точность. Помимо русских терминов в работе используются и их английские эквиваленты для понимания, под какими названиями искать численные процедуры в библиотеках и что означают их параметры.
Основные определения и простейшие свойства
Определитель
Введем определение определителя квадратной матрицы любого порядка. Это определение будет рекуррентным , то есть чтобы установить, что такое определитель матрицы порядка , нужно уже знать, что такое определитель матрицы порядка . Отметим также, что определитель существует только у квадратных матриц.
Определитель квадратной матрицы будем обозначать или det .
Определение 1.
Определителем
квадратной матрицы  второго порядка называется число
второго порядка называется число ![]() .
.
Определителем  квадратной матрицы порядка , называется число
квадратной матрицы порядка , называется число 
где - определитель матрицы порядка , полученной из матрицы вычеркиванием первой строки и столбца с номером .
Для наглядности запишем, как можно вычислить определитель матрицы четвертого порядка: 
Замечание. Реальное вычисление определителей для матриц выше третьего порядка на основе определения используется в исключительных случаях. Как правило, вычисление ведется по другим алгоритмам, которые будут рассмотрены позже и которые требуют меньше вычислительной работы.
Замечание. В определении 1 было бы точнее сказать, что определитель есть функция, определенная на множестве квадратных матриц порядка и принимающая значения в множестве чисел.
Замечание. В литературе вместо термина "определитель" используется также термин "детерминант", имеющий тот же самый смысл. От слова "детерминант" и появилось обозначение det .
Рассмотрим некоторые свойства определителей, которые сформулируем в виде утверждений.
Утверждение 1. При транспонировании матрицы определитель не меняется, то есть .
Утверждение 2. Определитель произведения квадратных матриц равен произведению определителей сомножителей, то есть .
Утверждение 3. Если в матрице поменять местами две строки, то ее определитель сменит знак.
Утверждение 4. Если матрица имеет две одинаковые строки, то ее определитель равен нулю.
В дальнейшем нам потребуется складывать строки и умножать строку на число. Эти действия над строками (столбцами) мы будем выполнять так же, как действия над матрицами-строками (матрицами-столбцами), то есть поэлементно. Результатом будет служить строка (столбец), как правило, не совпадающая со строками исходной матрицы. При наличии операций сложения строк (столбцов) и умножения их на число мы можем говорить и о линейных комбинациях строк (столбцов), то есть суммах с числовыми коэффициентами.
Утверждение 5. Если строку матрицы умножить на число , то ее определитель умножится на это число.
Утверждение 6. Если матрица содержит нулевую строку, то ее определитель равен нулю.
Утверждение 7. Если одна из строк матрицы равна другой, умноженной на число (строки пропорциональны), то определитель матрицы равен нулю.
Утверждение 8. Пусть в матрице i-ая строка имеет вид . Тогда , где матрица получается из матрицы заменой i-ой строки на строку , а матрица - заменой i-ой строки на строку .
Утверждение 9. Если к одной из строк матрицы добавить другую, умноженную на число, то определитель матрицы не изменится.
Утверждение 10. Если одна из строк матрицы является линейной комбинацией других ее строк, то определитель матрицы равен нулю.
Определение 2. Алгебраическим дополнением к элементу матрицы называется число, равное , где - определитель матрицы, полученной из матрицы вычеркиванием i-ой строки и j-ого столбца. Алгебраическое дополнение к элементу матрицы обозначается .
Пример.
Пусть  .
Тогда
.
Тогда 

Замечание.
Используя алгебраические дополнения, определение 1 определителя можно записать так: 
Утверждение 11. Разложение определителя по произвольной строке.
Для определителя матрицы справедлива формула 
Пример.
Вычислите  .
.
Решение.
Воспользуемся разложением по третьей строке, так выгоднее, поскольку в третьей строке два числа из трех - нули. Получим 
Утверждение 12.
Для квадратной матрицы порядка при выполнено соотношение  .
.
Утверждение 13.
Все свойства определителя, сформулированные для строк (утверждения 1 - 11), справедливы и для столбцов, в частности, справедливо разложение определителя по j-ому столбцу  и равенство
и равенство  при .
при .
Утверждение 14. Определитель треугольной матрицы равен произведению элементов ее главной диагонали.
Следствие. Определитель единичной матрицы равен единице, .
Вывод. Перечисленные выше свойства позволяют находить определители матриц достаточно высоких порядков при сравнительно небольшом объеме вычислений. Алгоритм вычислений следующий.
Алгоритм создания нулей в столбце. Пусть требуется вычислить определитель порядка . Если , то поменяем местами первую строку и любую другую, в которой первый элемент не нуль. В результате определитель , будет равен определителю новой матрицы с противоположным знаком. Если же первый элемент каждой строки равен нулю, то матрица имеет нулевой столбец и по утверждениям 1, 13 ее определитель равен нулю.
Итак, считаем, что уже в исходной матрице . Первую строку оставляем без изменений. Прибавим ко второй строке первую строку, умноженную на число . Тогда первый элемент второй строки будет равен  .
.
Остальные элементы новой второй строки обозначим , . Определитель новой матрицы по утверждению 9 равен .
Первую строку умножим на число и прибавим к третьей. Первый элемент новой третьей строки будет равен 
Остальные элементы новой третьей строки обозначим , . Определитель новой матрицы по утверждению 9 равен .
Процесс получения нулей вместо первых элементов строк продолжим дальше. Наконец, первую строку умножим на число и прибавим к последней строке. В результате получается матрица, обозначим ее , которая имеет вид 
причем . Для вычисления определителя матрицы используем разложение по первому столбцу
Так как , то 
В правой части стоит определитель матрицы порядка . К нему применим тот же алгоритм, и вычисление определителя матрицы сведется к вычислению определителя матрицы порядка . Процесс повторяем до тех пор, пока не дойдем до определителя второго порядка, который вычисляется по определению.
Если матрица не обладает какими-то специфическими свойствами, то заметно уменьшить объем вычислений по сравнению с предложенным алгоритмом не удается. Еще одна хорошая сторона этого алгоритма - по нему легко составить программу для компьютера для вычисления определителей матриц больших порядков. В стандартных программах вычисления определителей используется этот алгоритм с не принципиальными изменениями, связанными с минимизацией влияния ошибок округления и погрешностей входных данных при вычислениях компьютера.
Пример.
Вычислите определитель матрицы  .
.
Решение. Первую строку оставляем без изменения. Ко второй строке прибавляем первую, умноженную на число :
Определитель не меняется. К третьей строке прибавляем первую, умноженную на число :
Определитель не меняется. К четвертой строке прибавляем первую, умноженную на число :
Определитель не меняется. В результате получаем 
По тому же алгоритму считаем определитель матрицы порядка 3, стоящий справа. Первую строку оставляем без изменений, ко второй строке прибавляем первую, умноженную на число  :
:
К третьей строке прибавляем первую, умноженную на число  :
:
В результате получаем 
Ответ. .
Замечание. Хотя при вычислениях использовались дроби, результат оказался целым числом. Действительно, используя свойства определителей и то, что исходные числа - целые, операций с дробями можно было бы избежать. Но в инженерной практике числа крайне редко бывают целыми. Поэтому, как правило, элементы определителя будут десятичными дробями и применять какие-то ухищрения для упрощения вычислений нецелесообразно.
Обратная матрица
Определение 3. Матрица называется обратной матрицей для квадратной матрицы , если .
Из определения следует, что обратная матрица будет квадратной матрицей того же порядка, что и матрица (иначе одно из произведений или было бы не определено).
Обратная матрица для матрицы обозначается . Таким образом, если существует, то .
Из определения обратной матрицы следует, что матрица является обратной для матрицы , то есть . Про матрицы и можно говорить, что они обратны друг другу или взаимно обратны.
Если определитель матрицы равен нулю, то обратная к ней не существует.
Так как для нахождения обратной матрицы важно, равен ли определитель марицы нулю или нет, то введем следующие определения.
Определение 4. Квадратную матрицу назовем вырожденной или особенной матрицей , если , и невырожденной или неособенной матрицей , если .
Утверждение. Если обратная матрица существует, то она единственна.
Утверждение.
Если квадратная матрица является невырожденной, то обратная для нее существует и  (1)
где - алгебраические дополнения к элементам .
(1)
где - алгебраические дополнения к элементам .
Теорема. Обратная матрица для квадратной матрицы существует тогда и только тогда, когда матрица - невырожденная, обратная матрица единственна, и справедлива формула (1).
Замечание. Следует обратить особое внимание на места, занимаемые алгебраическими дополнениями в формуле обратной матрицы: первый индекс показывает номер столбца , а второй - номер строки , в которые нужно записать вычисленное алгебраическое дополнение.
Пример.
 .
.
Решение. Находим определитель
Так как , то матрица - невырожденная, и обратная для нее существует.
Находим алгебраические дополнения: 
Составляем обратную матрицу, размещая найденные алгебраические дополнения так, чтобы первый индекс соответствовал столбцу, а второй - строке:  (2)
(2)
Полученная матрица (2) и служит ответом к задаче.
Замечание.
В предыдущем примере было бы точнее ответ записать так:  (3)
(3)
Однако запись (2) более компактна и с ней удобнее проводить дальнейшие вычисления, если таковые потребуются. Поэтому запись ответа в виде (2) предпочтительнее, если элементы матриц - целые числа. И наоборот, если элементы матрицы - десятичные дроби, то обратную матрицу лучше записать без множителя впереди.
Замечание. При нахождении обратной матрицы приходится выполнять довольно много вычислений и необычно правило расстановки алгебраических дополнений в итоговой матрице. Поэтому велика вероятность ошибки. Чтобы избежать ошибок следует делать проверку: вычислить произведение исходной матрицы на итоговую в том или ином порядке. Если в результате получится единичная матрица, то обратная матрица найдена правильно. В противном случае нужно искать ошибку.
Пример.
Найдите обратную матрицу для матрицы  .
.
Решение.
![]() - существует.
- существует.
Ответ:
 .
.
Вывод. Нахождение обратной матрицы по формуле (1) требует слишком много вычислений. Для матриц четвертого порядка и выше это неприемлемо. Реальный алгоритм нахождения обратной матрицы будет приведен позже.
Вычисление определителя и обратной матрицы с помощью метода Гаусса
Метод Гаусса можно использовать для нахождения определителя и обратной матрицы .
Именно, определитель матрицы равен det .
Обратная матрица находится решением систем линейных уравнений методом исключения Гаусса:
Где есть j-тый столбец единичной матрицы , - искомый вектор.
Полученные векторы решений - образуют, очевидно, столбцов матрицы , поскольку .
Формулы для определителя
1. Если матрица невырожденная, то и (произведение ведущих элементов).
Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.
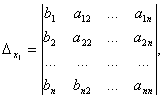
Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).
Определители
получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:
 ;
;
 .
.
Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.
Пример 1. Решить систему линейных уравнений:
Согласно теореме Крамера имеем:


Итак, решение системы (2):
онлайн-калькулятором , решающим методом Крамера.
Три случая при решении систем линейных уравнений
Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение
(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений
(система совместна и неопределённа)
** ![]() ,
,
т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет
(система несовместна)
Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .
Примеры решения систем линейных уравнений методом Крамера
Пусть дана система
 .
.
На основании теоремы Крамера
………….
,
где -
-
определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:


Пример 2.
 .
.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители


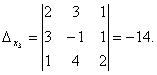
По формулам Крамера находим:
![]()
Итак, (1; 0; -1) – единственное решение системы.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.
Пример 3. Решить систему линейных уравнений методом Крамера:
 .
.
Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных



По формулам Крамера находим:
Итак, решение системы - (2; -1; 1).
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
К началу страницы
Продолжаем решать системы методом Крамера вместе
Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.
Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных



Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных - буквы. За примерами далеко ходить не надо.
Следующий пример - на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.
Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных







