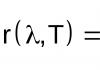Помощь по Теле2, тарифы, вопросы

Урок математики по теме “Показательная функция”10 класс (учебник “Алгебра и начала математического анализа 10 класс” С.М. Никольский, М.К. Потапов и др.) разработан с использованием компьютерных технологий.

На уроке рассматривается функция , где , рассматриваются свойства этой функции и ее график. Эти свойства будут использоваться в дальнейшем, при доказательстве свойств логарифмической функции, при решении показательных уравнений и неравенств.

Тип урока: комбинированный с применением компьютера и интерактивной доски.

Компьютерные технологии создают большие возможности активизации учебной деятельности. Широкое применение ИКТ при изучении большинства предметов дает возможность реализовать принцип “учение с увлечением”, и тогда любой предмет будет иметь равные шансы стать любимым детьми.

Место данного урока в теме: первый урок в теме.

Метод: комбинированный (словесно-наглядно-практический).

Цель урока: сформировать представление о показательной функции, ее свойствах и графиках.

Задачи урока:

• научить строить простейшие графики показательной функции и решать показательные уравнения графически,
• научить применять свойства показательной функции,
• осуществить контроль знаний,
• использовать различные приемы и методы для поддержания работоспособности учащихся.

Материал для урока подобран таким образом, что предполагает работу с учащихся различных категорий - от слабых учеников до сильных.

Ход урока

I. Организационный момент (слайд 1-4). Презентация

II. Изучение нового материала (слайд 5-6)

Определение показательной функции;

Свойства показательной функции;

График показательной функции.

III. Устно - закрепление новых знаний (слайды 7-16)

1) Выяснить, является ли функция возрастающей (убывающей)

2) Сравнить: .

3) Сравнить с единицей:

4) На рисунке изображены графики показательных функций. Соотнесите график функции с формулой.

IV. Динамическая пауза

V. Обобщение и систематизация новых знаний (слайд 16-20)

1) Построить график функции: y=(1/3) x ;

2) Решить графически уравнение:

3) Применение показательной функции к решению прикладных задач:

“Период полураспада плутония равен 140 суткам. Сколько плутония останется через 10 лет, если его начальная масса равна 8 г?”

VI. Тестовая работа (слайд 21)

Каждый ученик имеет карточку с заданием - тест (Приложение 1) и таблицу для внесения ответов (Приложение 2).

Проверяем и оцениваем (слайд 22)

VII. Домашнее задание (слайд 23-24)

№ 4.55 (а, в, и) № 4.59, № 4.60 (а, ж); № 4.61 (г, з)

Задача (для тех, кто интересуется математикой):

Зависимость давления атмосферы р (в сантиметрах ртутного столба) от выраженной в километрах высоты h над уровнем моря выражается формулой

Вычислить, каким будет атмосферное давление на вершине Эльбруса, высота которой 5,6 км?

VIII. Подведение итогов

Литература

1. С.М.Никольский, М. К. Потапов и др. “Алгебра и начала математического анализа 10 класс”, Москва “ Просвещение”, 2010.
2. М. К. Потапов, А.В. Потапов “Алгебра и начала математического анализа 10 класс. Книга для учителя”, Москва “ Просвещение”, 2009.
3. М. К. Потапов, А.В. Потапов “Алгебра и начала математического анализа 10 класс. Дидактические материалы”, Москва “ Просвещение”, 2009.
4. Л. О. Денищева и др. “Сборник экзаменационных заданий. Математика. ЭГЕ”, Москва, издательство “Эксмо”, 2009.
5. Математика. Сборник тренировочных работ. Под редакцией А.Л. Семенова, И. В. Ященко, Москва, “Экзамен”, 2009.

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

МАОУ «Сладковская СОШ» Показательная функция, её свойства и график 10 класс

Функция вида у = а х,где а - заданное число, а > 0, а ≠ 1, х-переменная, называется показательной.

Показательная функция обладает следующими свойствами: О.О.Ф: множество R всех действительных чисел; Мн.зн.: множество всех положительных чисел; Показательная функция у=а х является возрастающей на множестве всех действительных чисел,если а>1 ,и убывающей,если 0

Графики функции у=2 х и у=(½) х 1.График функции у=2 х проходит через точку (0;1) и расположен выше оси Ох. а>1 Д(у): х є R Е(у): у > 0 Возрастает на всей области определения. 2. График функции у= также проходит через точку (0;1) и расположен выше оси Ох. 0

Используя свойства возрастания и убывания показательной функции, можно сравнить числа и решать показательные неравенства. Сравнить: а) 5 3 и 5 5 ; б) 4 7 и 4 3 ; в) 0,2 2 и 0,2 6 ; г) 0,9 2 и 0,9. Решить: а) 2 х >1; б) 13 х+1 0,7; г) 0,04 х а в или а х 1, то х>в (х

Решить графически уравнения: 1) 3 x =4-x, 2) 0,5 х =х+3.

Если снять кипящий чайник с огня, то сначала он быстро остывает, а потом остывание идет гораздо медленнее, это явление описывается формулой T =(T 1 - T 0) e - kt + T 1 Применение показательной функции в жизни, науке и технике

Рост древесины происходит по закону: A - изменение количества древесины во времени; A 0 - начальное количество древесины; t -время, к, а- некоторые постоянные. Давление воздуха убывает с высотой по закону: P - давление на высоте h, P0 - давление на уровне моря, а - некоторая постоянная.

Рост народонаселения Изменение числа людей в стране на небольшом отрезке времени описывается формулой, где N 0 - число людей в момент времени t=0, N -число людей в момент времени t, a -константа.

Закон органического размножения: при благоприятных условиях (отсутствие врагов, большое количество пищи) живые организмы размножались бы по закону показательной функции. Например: одна комнатная муха может за лето произвести 8 х 10 14 особей потомства. Их вес составил бы несколько миллионов тонн (а вес потомство пары мух превысил бы вес нашей планеты), они бы заняли огромное пространство,а если выстроить их в цепочку, то её длинна будет больше, чем расстояние от Земли до Солнца. Но так как, кроме мух существует множество других животных и растений, многие из которых являются естественными врагами мух их количество не достигает вышеуказанных значений.

Когда радиоактивное вещество распадается, его количество уменьшается, через некоторое время остается половина от первоначального вещества. Этот промежуток времени t 0 называется периодом полураспада. Общая формула для этого процесса: m = m 0 (1/2) -t/t 0 , где m 0 - первоначальная масса вещества. Чем больше период полураспада, тем медленнее распадается вещество. Это явление используют для определения возраста археологических находок. Радий, например, распадается по закону: M = M 0 e -kt . Используя данную формулу ученые рассчитали возраст Земли (радий распадается примерно за время, равное возрасту Земли).

По теме: методические разработки, презентации и конспекты

Применение интеграции в учебном процессе как способа развития аналитических и творческих способностей....

Данная презентация предназначена для повторения темы «Показательная функция» в 10 классе. Она содержит как теоретические сведения по данной теме, так и разноуровневые практические задания. Разработка состоит из трёх блоков:

1. Рассмотрение основных свойств показательной функции.
2. Решение показательных уравнений.
3. Решение показательных неравенств.

В презентации показаны различные способы решения показательных уравнений и неравенств. Данную разработку можно использовать не только при объяснении отдельных тем, но и при подготовке к экзамену.

Скачать:

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

«Показательная функция» Учитель математики МАОУ лицей №3 города Кропоткин Краснодарского края Зозуля Елена Алексеевна

Определение Показательная функция – это функция вида, где x – переменная, - заданное число, >0,  1. Примеры:

Свойства показательной функции Область определения: все действительные числа Множество значений: все положительные числа При > 1 функция возрастающая; при 0

График показательной функции Т.к. , то график любой показательной функции проходит через точку (0; 1) 1 1 х х у у 0 0

Показательные уравнения Определение Простейшие уравнения Способы решения сложных уравнений

Определение Уравнение, в котором переменная содержится в показателе степени, называется показательным. Примеры:

Простейшее показательное уравнение – это уравнение вида Простейшее показательное уравнение решается с использованием свойств степени.

Способы решения сложных показательных уравнений. Вынесение за скобки степени с меньшим показателем Замена переменной Деление на показательную функцию

Вынесение за скобки степени с меньшим показателем Данный способ используется, если соблюдаются два условия: 1) основания степеней одинаковы; 2) коэффициенты перед переменной одинаковы Например:

Замена переменной При данном способе показательное уравнение сводится к квадратному. Способ замены переменной используют, если показатель одной из степеней в 2 раза больше, чем у другой. Например: 3 2 x – 4 · 3 х – 45 = 0 коэффициенты перед переменной противоположны. Н апример: 2 2 - х – 2 х – 1 =1 б) а) основания степеней одинаковы;

Деление на показательную функцию Данный способ используется, если основания степеней разные. а) в уравнении вида a x = b x делим на b x Например: 2 х = 5 х | : 5 x б) в уравнении A a 2 x + B (ab) x + C b 2 x = 0 делим на b 2x . Например: 3  25 х - 8  15 х + 5  9 х = 0 | : 9 x

Показательные неравенства Определение Простейшие неравенства Решение неравенств

Определение Показательные неравенства – это неравенства, в которых неизвестное содержится в показателе степени. Примеры:

Простейшие показательные неравенства – это неравенства вида: где a > 0, a  1, b – любое число.

При решении простейших неравенств используют свойства возрастания или убывания показательной функции. Для решения более сложных показательных неравенств используются те же способы, что и при решении показательных уравнений.

Показательная функция Построение графика Сравнение чисел с использованием свойств показательной функции Сравнение числа с 1 а) аналитический способ; б) графический способ.

Задача 1 Построить график функции y = 2 x x y -1 8 7 6 5 4 3 2 1 - 3 - 2 -1 0 1 2 3 х у 3 8 2 4 1 2 0 1

Задача 2 Сравнить числа Решение Ответ:

Задача 3 Сравнить число с 1. Решение -5

Задача 4 C равнить число р с 1 р = 2 > 1 , то функция у = 2 t – возрастающая. 0 1. Ответ: > 1 р =

Решение показательных уравнений Простейшие показательные уравнения Уравнения, решаемые вынесением за скобки степени с меньшим показателем Уравнения, решаемые заменой переменной случай 1; случай 2. Уравнения, решаемые делением на показательную функцию случай 1; случай 2.

Простейшие показательные уравнения Ответ: - 5,5 . Ответ: 0; 3.

Вынесение за скобки степени с меньшим показателем Ответ: 5 x + 1 - (x - 2) = = x + 1 – x + 2 = 3

Замена переменной (1) основания степеней одинаковы, показатель одной из степеней в 2 раза больше, чем у другой. 3 2 x – 4 · 3 х – 45 = 0 t = 3 x (t > 0) t 2 – 4 t – 45 = 0 По т. Виета: t 1 · t 2 = - 45; t 1 + t 2 = 4 t 1 = 9 ; t 2 = - 5 – не удовлетворяет условию 3 x = 9 ; 3 x = 3 2 ; x = 2 . Ответ: 2

Замена переменной (2) Основания степеней одинаковы, коэффициенты перед переменной противоположны. По т. Виета: - Не удовлетворяет условию Ответ: 1

Деление на показательную функцию Ответ: 0

Деление на показательную функцию Ответ: 0; 1.

Простейшие показательные неравенства Двойные неравенства Неравенства, решаемые вынесением за скобки степени с меньшим показателем Неравенства, решаемые заменой переменной Решение показательных неравенств

Простейшие показательные неравенства

Двойные неравенства Ответ: (- 4; -1). 3 > 1 , то

Решение показательных неравенств Метод: Вынесение за скобки степени с меньшим показателем Ответ: х > 3 Т.к. 3 > 1 , то знак неравенства остается прежним: 10

Решение показательных неравенств Метод: Замена переменной Ответ: х 1 , то

Используемая литература. А.Г.Мордкович: Алгебра и начала математического анализа(профильный уровень), 10класс,2011г. А.Н. Колмогоров: Алгебра и начала математического анализа,2008г. Интернет

Основные свойства а>10 10"> 10"> 10" title="Основные свойства а>10"> title="Основные свойства а>10">

График функции Кривая называется экспонентой а>1 0 1 0"> 1 0"> 1 0" title="График функции Кривая называется экспонентой а>1 0"> title="График функции Кривая называется экспонентой а>1 0">

Геометрическая особенность графика функции Ось Ох является горизонтальной асимптотой графика функции при х -, если а >1 при х -, если а >1 при х +, если 0 1 при х -, если а >1 при х +, если 0"> 1 при х -, если а >1 при х +, если 0"> 1 при х -, если а >1 при х +, если 0" title="Геометрическая особенность графика функции Ось Ох является горизонтальной асимптотой графика функции при х -, если а >1 при х -, если а >1 при х +, если 0"> title="Геометрическая особенность графика функции Ось Ох является горизонтальной асимптотой графика функции при х -, если а >1 при х -, если а >1 при х +, если 0">

Показательными уравнениями называют уравнения вида а>0,а1, и уравнения, сводящиеся к этому виду 0,а1, и уравнения, сводящиеся к этому виду"> 0,а1, и уравнения, сводящиеся к этому виду"> 0,а1, и уравнения, сводящиеся к этому виду" title="Показательными уравнениями называют уравнения вида а>0,а1, и уравнения, сводящиеся к этому виду"> title="Показательными уравнениями называют уравнения вида а>0,а1, и уравнения, сводящиеся к этому виду">

Основные методы решения показательных уравнений Функционально-графический Функционально-графический Основан на использовании графический иллюстраций или каких- либо свойств функции. Метод уравнивания показателей Метод уравнивания показателей Основан на применении теоремы: Уравнение равносильно уравнению f(x)=g(x), где а>0,а1. Метод введения новой переменной Метод введения новой переменной 0,а1. Метод введения новой переменной Метод введения новой переменной">

0,а1, и неравенства, сводящиеся к этому виду. Теорема: Показательное неравенство равносильно неравенству f(x)>g(x), если а >1 ; Показательное неравенство равносильно н" title="Показательные неравенства Показательными неравенствами называют неравенства вида а>0,а1, и неравенства, сводящиеся к этому виду. Теорема: Показательное неравенство равносильно неравенству f(x)>g(x), если а >1 ; Показательное неравенство равносильно н" class="link_thumb"> 8 Показательные неравенства Показательными неравенствами называют неравенства вида а>0,а1, и неравенства, сводящиеся к этому виду. Теорема: Показательное неравенство равносильно неравенству f(x)>g(x), если а >1 ; Показательное неравенство равносильно неравенству f(x) 0,а1, и неравенства, сводящиеся к этому виду. Теорема: Показательное неравенство равносильно неравенству f(x)>g(x), если а >1 ; Показательное неравенство равносильно н"> 0,а1, и неравенства, сводящиеся к этому виду. Теорема: Показательное неравенство равносильно неравенству f(x)>g(x), если а >1 ; Показательное неравенство равносильно неравенству f(x) "> 0,а1, и неравенства, сводящиеся к этому виду. Теорема: Показательное неравенство равносильно неравенству f(x)>g(x), если а >1 ; Показательное неравенство равносильно н" title="Показательные неравенства Показательными неравенствами называют неравенства вида а>0,а1, и неравенства, сводящиеся к этому виду. Теорема: Показательное неравенство равносильно неравенству f(x)>g(x), если а >1 ; Показательное неравенство равносильно н"> title="Показательные неравенства Показательными неравенствами называют неравенства вида а>0,а1, и неравенства, сводящиеся к этому виду. Теорема: Показательное неравенство равносильно неравенству f(x)>g(x), если а >1 ; Показательное неравенство равносильно н">

Свойства функции Проанализируем по схеме: Проанализируем по схеме: 1. область определения функции 1. область определения функции 2. множество значений функции 2. множество значений функции 3. нули функции 3. нули функции 4. промежутки знакопостоянства функции 4. промежутки знакопостоянства функции 5. четность или нечётность функции 5. четность или нечётность функции 6. монотонность функции 6. монотонность функции 7. наибольшее и наименьшее значения 7. наибольшее и наименьшее значения 8. периодичность функции 8. периодичность функции 9. ограниченность функции 9. ограниченность функции

0 при х R. 5) Функция ни чётная, ни " title="Показательная функция, её график и свойства y x 1 о 1) Область определения – множество всех действительных чисел (D(у)=R). 2) Множество значений – множество всех положительных чисел (E(y)=R +). 3) Нулей нет. 4) у>0 при х R. 5) Функция ни чётная, ни " class="link_thumb"> 10 Показательная функция, её график и свойства y x 1 о 1) Область определения – множество всех действительных чисел (D(у)=R). 2) Множество значений – множество всех положительных чисел (E(y)=R +). 3) Нулей нет. 4) у>0 при х R. 5) Функция ни чётная, ни нечётная. 6) Функция монотонна: возрастает на R при а>1 и убывает на R при 0 0 при х R. 5) Функция ни чётная, ни "> 0 при х R. 5) Функция ни чётная, ни нечётная. 6) Функция монотонна: возрастает на R при а>1 и убывает на R при 0"> 0 при х R. 5) Функция ни чётная, ни " title="Показательная функция, её график и свойства y x 1 о 1) Область определения – множество всех действительных чисел (D(у)=R). 2) Множество значений – множество всех положительных чисел (E(y)=R +). 3) Нулей нет. 4) у>0 при х R. 5) Функция ни чётная, ни "> title="Показательная функция, её график и свойства y x 1 о 1) Область определения – множество всех действительных чисел (D(у)=R). 2) Множество значений – множество всех положительных чисел (E(y)=R +). 3) Нулей нет. 4) у>0 при х R. 5) Функция ни чётная, ни ">

Рост древесины происходит по закону, где: A- изменение количества древесины во времени; A 0 - начальное количество древесины; t-время, к, а- некоторые постоянные. Рост древесины происходит по закону, где: A- изменение количества древесины во времени; A 0 - начальное количество древесины; t-время, к, а- некоторые постоянные. t 0 t0t0 t1t1 t2t2 t3t3 tntn А A0A0 A1A1 A2A2 A3A3 AnAn

Температура чайника изменяется по закону, где: Т- изменение температуры чайника со временем; Т 0 - температура кипения воды; t-время, к, а- некоторые постоянные. Температура чайника изменяется по закону, где: Т- изменение температуры чайника со временем; Т 0 - температура кипения воды; t-время, к, а- некоторые постоянные. t 0 t0t0 t1t1 t2t2 t3t3 tntn T T0T0 T1T1 T2T2 T3T3

Радиоактивный распад происходит по закону, где: Радиоактивный распад происходит по закону, где: N- число нераспавшихся атомов в любой момент времени t; N 0 - начальное число атомов (в момент времени t=0); t-время; N- число нераспавшихся атомов в любой момент времени t; N 0 - начальное число атомов (в момент времени t=0); t-время; Т- период полураспада. Т- период полураспада. t 0 t 1 t 2 N N3N3 N4N4 t4t4 N0N0 t3t3 N2N2 N1N1

С Существенное свойство процессов органического и изменения величин состоит в том, что за равные промежутки времени значение величины изменяется в одном и том же отношении Рост древесины Изменение температуры чайника Изменение давления воздуха К процессам органического изменения величин относятся: Радиоактивный распад

Сравните числа 1,3 34 и 1,3 40. Пример 1. Сравните числа 1,3 34 и 1,3 40. Общий метод решения. 1. Представить числа в виде степени с одинаковым основанием (если это необходимо) 1,3 34 и 1, Выяснить, возрастающей или убывающей является показательная функция а=1,3; а>1, след-но показательная функция возрастает. а=1,3; а>1, след-но показательная функция возрастает. 3. Сравнить показатели степеней (или аргументы функций) 34 1, след-но показательная функция возрастает. а=1,3; а>1, след-но показательная функция возрастает. 3. Сравнить показатели степеней (или аргументы функций) 34">

Решите графически уравнение 3 х =4-х. Пример 2. Решите графически уравнение 3 х =4-х.Решение. Используем функционально-графический метод решения уравнений: построим в одной системе координат графики функций у=3 х и у=4-х. графики функций у=3 х и у=4-х. Замечаем, что они имеют одну общую точку (1;3). Значит, уравнение имеет единственный корень х=1. Ответ: 1 Ответ: 1 у=4-х

4-х. Пример 3. Решите графически неравенство 3 х >4-х. Решение. у=4-х Используем функционально-графический метод решения неравенств: 1. Построим в одной системе 1. Построим в одной системе координат графики функций " title="Решите графически неравенство 3 х >4-х. Пример 3. Решите графически неравенство 3 х >4-х. Решение. у=4-х Используем функционально-графический метод решения неравенств: 1. Построим в одной системе 1. Построим в одной системе координат графики функций " class="link_thumb"> 24 Решите графически неравенство 3 х >4-х. Пример 3. Решите графически неравенство 3 х >4-х. Решение. у=4-х Используем функционально-графический метод решения неравенств: 1. Построим в одной системе 1. Построим в одной системе координат графики функций координат графики функций у=3 х и у=4-х. 2. Выделим часть графика функции у=3 х, расположенную выше (т. к. знак >) графика функции у=4-х. 3. Отметим на оси х ту часть, которая соответствует выделенной части графика (иначе: спроецируем выделенную часть графика на ось х). 4. Запишем ответ в виде интервала: Ответ: (1;). Ответ: (1;). 4-х. Пример 3. Решите графически неравенство 3 х >4-х. Решение. у=4-х Используем функционально-графический метод решения неравенств: 1. Построим в одной системе 1. Построим в одной системе координат графики функций "> 4-х. Пример 3. Решите графически неравенство 3 х >4-х. Решение. у=4-х Используем функционально-графический метод решения неравенств: 1. Построим в одной системе 1. Построим в одной системе координат графики функций координат графики функций у=3 х и у=4-х. 2. Выделим часть графика функции у=3 х, расположенную выше (т. к. знак >) графика функции у=4-х. 3. Отметим на оси х ту часть, которая соответствует выделенной части графика (иначе: спроецируем выделенную часть графика на ось х). 4. Запишем ответ в виде интервала: Ответ: (1;). Ответ: (1;)."> 4-х. Пример 3. Решите графически неравенство 3 х >4-х. Решение. у=4-х Используем функционально-графический метод решения неравенств: 1. Построим в одной системе 1. Построим в одной системе координат графики функций " title="Решите графически неравенство 3 х >4-х. Пример 3. Решите графически неравенство 3 х >4-х. Решение. у=4-х Используем функционально-графический метод решения неравенств: 1. Построим в одной системе 1. Построим в одной системе координат графики функций "> title="Решите графически неравенство 3 х >4-х. Пример 3. Решите графически неравенство 3 х >4-х. Решение. у=4-х Используем функционально-графический метод решения неравенств: 1. Построим в одной системе 1. Построим в одной системе координат графики функций ">

Решите графически неравенства: 1) 2 х >1; 2) 2 х 1; 2) 2 х "> 1; 2) 2 х "> 1; 2) 2 х " title="Решите графически неравенства: 1) 2 х >1; 2) 2 х "> title="Решите графически неравенства: 1) 2 х >1; 2) 2 х ">

Самостоятельная работа (тест) 1. Укажите показательную функцию: 1. Укажите показательную функцию: 1) у=х 3 ; 2) у=х 5/3 ; 3) у=3 х+1 ; 4) у=3 х+1. 1) у=х 3 ; 2) у=х 5/3 ; 3) у=3 х+1 ; 4) у=3 х+1. 1) у=х 2 ; 2) у=х -1 ; 3) у=-4+2 х; 4) у=0,32 х. 1) у=х 2 ; 2) у=х -1 ; 3) у=-4+2 х; 4) у=0,32 х. 2. Укажите функцию, возрастающую на всей области определения: 2. Укажите функцию, возрастающую на всей области определения: 1) у =(2/3) -х; 2) у=2 -х; 3) у =(4/5) х; 4) у =0,9 х. 1) у =(2/3) -х; 2) у=2 -х; 3) у =(4/5) х; 4) у =0,9 х. 1) у =(2/3) х; 2) у=7,5 х; 3) у =(3/5) х; 4) у =0,1 х. 1) у =(2/3) х; 2) у=7,5 х; 3) у =(3/5) х; 4) у =0,1 х. 3. Укажите функцию, убывающую на всей области определения: 3. Укажите функцию, убывающую на всей области определения: 1) у =(3/11) -х; 2) у=0,4 х; 3) у =(10/7) х; 4) у =1,5 х. 1) у =(2/17) -х; 2) у=5,4 х; 3) у =0,7 х; 4) у =3 х. 4. Укажите множество значений функции у=3 -2 х -8: 4. Укажите множество значений функции у=2 х+1 +16: 5. Укажите наименьшее из данных чисел: 5. Укажите наименьшее из данных чисел: 1) 3 -1/3 ; 2) 27 -1/3 ; 3) (1/3) -1/3 ; 4) 1 -1/3. 1) 3 -1/3 ; 2) 27 -1/3 ; 3) (1/3) -1/3 ; 4) 1 -1/3. 5. Укажите наибольшее из данных чисел: 1) 5 -1/2 ; 2) 25 -1/2 ; 3) (1/5) -1/2 ; 4) 1 -1/2. 1) 5 -1/2 ; 2) 25 -1/2 ; 3) (1/5) -1/2 ; 4) 1 -1/2. 6. Выясните графически, сколько корней имеет уравнение 2 х =х -1/3 (1/3) х =х 1/2 6. Выясните графически, сколько корней имеет уравнение 2 х =х -1/3 (1/3) х =х 1/2 1) 1 корень; 2) 2 корня; 3) 3 корня; 4) 4 корня.

1. Укажите показательную функцию: 1) у=х 3; 2) у=х 5/3; 3) у=3 х+1; 4) у=3 х+1. 1) у=х 3; 2) у=х 5/3; 3) у=3 х+1; 4) у=3 х Укажите функцию, возрастающую на всей области определения: 2. Укажите функцию, возрастающую на всей области определения: 1) у =(2/3)-х; 2) у=2-х; 3) у =(4/5)х; 4) у =0,9 х. 1) у =(2/3)-х; 2) у=2-х; 3) у =(4/5)х; 4) у =0,9 х. 3. Укажите функцию, убывающую на всей области определения: 3. Укажите функцию, убывающую на всей области определения: 1) у =(3/11)-х; 2) у=0,4 х; 3) у =(10/7)х; 4) у =1,5 х. 1) у =(3/11)-х; 2) у=0,4 х; 3) у =(10/7)х; 4) у =1,5 х. 4. Укажите множество значений функции у=3-2 х-8: 4. Укажите множество значений функции у=3-2 х-8: 5. Укажите наименьшее из данных чисел: 5. Укажите наименьшее из данных чисел: 1) 3-1/3; 2) 27-1/3; 3) (1/3)-1/3; 4) 1-1/3. 1) 3-1/3; 2) 27-1/3; 3) (1/3)-1/3; 4) 1-1/3. 6. Выясните графически, сколько корней имеет уравнение 2 х=х- 1/3 6. Выясните графически, сколько корней имеет уравнение 2 х=х- 1/3 1) 1 корень; 2) 2 корня; 3) 3 корня; 4) 4 корня. 1) 1 корень; 2) 2 корня; 3) 3 корня; 4) 4 корня. Проверочная работа Выберите показательные функции, которые: Выберите показательные функции, которые: I вариант – убывают на области определения; I вариант – убывают на области определения; II вариант – возрастают на области определения. II вариант – возрастают на области определения.