Помощь по Теле2, тарифы, вопросы

I.Условные вероятности. Априорная и апостериорная вероятность. 3

II.Независимые события. 5

III.Проверка статистических гипотез. Статистическая достоверность. 7

IV.Использование критерия «хи-квадрат» 19

1.Определение достоверности отличия набора частот от набора вероятностей. 19

2.Определение достоверности отличия нескольких наборов частот. 26

VСАМОСТОЯТЕЛЬНОЕ ЗАДАНИЕ 33

Занятие №2

1. Условные вероятности. Априорная и апостериорная вероятность.

Случайная величина задается тремя объектами: множеством элементарных событий, множеством событий и вероятностью событий. Те значения,которые может принимать случайная величина, называютсяэлементарными событиями. Наборы элементарных событий называютсясобытиями . Для числовых и других не очень сложных случайных величин любой конкретно заданный набор элементарных событий есть событие.

Приведем пример: бросание игральной кости.

Всего имеется 6 элементарных событий: «очко», «2 очка», «3 очка»… «6 очков». Событие – любой набор элементарных событий, например «чет» -сумма элементарных событий «2 очка», «4 очка» и «6 очков».

Вероятность любого элементарного события P(A) равна 1/6:

вероятность события – количеству входящих в него элементарных событий, деленному на 6.

Достаточно часто в добавление к известной вероятности события имеется некоторая дополнительная информация, которая меняет эту вероятность. Например, летальность больных. поступивших в больницу с острой кровоточащей язвой желудка, составляет около 10%. Однако, если больному больше 80 лет, эта летальность составляет 30%.

Для описания таких ситуаций были введены так называемые условные вероятности . Они обозначаются, какP(A/B) и читаются «вероятность события А при условии события В». Для вычисления условной вероятности используется формула:

Вернемся к предыдущему примеру:

Пусть среди больных, поступивших в больницу с острой кровоточащей язвой желудка 20% - больные старше 80 лет. Причем, среди всех больных доля умерших больных старше 80 лет – 6%(напомним, что доля всех умерших составляет 10%). В этом случае

При определении условных вероятностей часто пользуются терминами априорной (буквально – до опыта) иапостериорной (буквально – после опыта) вероятности.

Пользуясь условными вероятностями, можно по одним вероятностям вычислить другие, например, менять местами событие и условие.

Рассмотрим эту технику на примере анализа связи риска заболевания ревматизма (ревматической лихорадкой) и одного из антигенов, являющихся для него фактором риска.

Частота заболевания ревматизмом – около 1%. Обозначим наличие ревматизма как R + , тогда какP(R +)=0,01.

Наличие антигена будем обозначать, как А + . Его находят у 95% больных ревматизмом и у 6% лиц, ревматизмом не болеющих. В наших обозначениях это: условные вероятности Р(А + /R +)=0,95 и Р(А + /R -)=0,06.

На основании этих трех вероятностей будем последовательно определять другие вероятности.

Прежде всего, если заболеваемость ревматизмом P(R +)=0,01, то вероятность не заболетьP(R -)=1-P(R +)=0,99.

Из формулы для условной вероятности находим, что

Р(А + иR +)= Р(А + /R +) * Р(R +) = 0,95*0,01 = 0,0095, или 0,95% популяции одновременно и болеют ревматизмом и имеют антиген.

Аналогично

Р(А + иR -)= Р(А + /R -) * Р(R -) = 0,06*0,99 = 0,0594, или 5,94% популяции носят антиген, но ревматизмом не болеют.

Так как все имеющие антиген или болеют ревматизмом или и не болеют (но не одновременно и то и другое), то сумма двух последних вероятностей дает частоту носительства антигена в популяции в целом:

Р(А +)= Р(А + иR +) + Р(А + иR -) = 0,0095 + 0,0594 = 0,0689

Соответственно, доля людей, не имеющих антиген равна

Р(А -)=1- Р(А +) = 0,9311

Так как заболеваемость ревматизмом равна 1%, а доля лиц, имеющих антиген и болеющих ревматизмом, равна 0,95%, то доля лиц, болеющих ревматизмом и не имеющих антигена равна:

Р(А - иR +) = Р(R +) - Р(А + иR +) = 0,01 – 0,0095 = 0,0005

Теперь будем двигаться в обратную сторону, переходя от вероятностей событий и их комбинаций к условным вероятностям. По исходной формуле условной вероятности Р(А + /R +)= Р(R + иA +)/ Р(А +) = 0,0095/0,06890,1379 , или примерно 13,8% лиц, носящих антиген, заболеют ревматизмом. Так как заболеваемость популяции в целом лишь 1%, то факт выявления антигена повышает вероятность заболевания ревматизмом в 14 раз.

Аналогичным образом Р(R + /А -)=Р(R + иA -)/ Р(А -) = 0,0005/0,93110,000054, то есть тот факт, что при проверке антигена не обнаружено, снижает вероятность заболевания ревматизмом в 19 раз.

Оформим эту задачу в электронной таблице Excel:

Можно посмотреть процесс построения таблицы картинки2\p2-1.gif

1)Выборка вероятностей всех симптомов для предполагаемых заболеваний. Если заболеваний три (D1,D2,D3), то должно появиться три группы чисел:

P(S 2 /D 1) P(S 2 /D 2) P(S 2 /D 3)

P(S 7 /D 1) P(S 7 /D 2) P(S 7 /D 3)

P(S 9 /D 1) P(S 9 /D 2) P(S 9 /D 3)

Если симптомов много и много возможных диагнозов, что и бывает на практике, то один этот этап выборки осуществить без привлечения ЭВМ принципиально невозможно, что и сделало данный метод возможным лишь с использованием компьютерных технологий.

2)Вычисление условной вероятности симптомокомплекса P(S сi /D j). Вычисляют по формуле, известной из теории вероятностей. Условная вероятность симптомокомплекса представляет собой произведение вероятностей симптомов данного симптомокомплекса при данном диагнозе. Например, для симптомокомплекса из n симптомов для некоторого диагноза J:

P(S ci /Dj)= P(S 1 /D j)*P(S 2 /D j) * ... * P(S n /D j) (1)

Количество получаемых таки образом условных вероятностей равно количеству рассматриваемых в системе диагнозов (т.е. числу столбцов таблицы).

Определение априорной вероятности заболевания.

Априорной вероятностью некоторого диагноза (Dj) называют эмпирическую частоту наблюдения данного заболевания в некоторых конкретных условиях. Априорная вероятность обозначается P(D j) .Она характеризует распределение болезней в данной группе населения. Такой группой может быть контингент данной больницы, данного района, данного города. Априорной (доопытной) она называется потому, что уже известна до получения симптомокомплекса, т.е. к ней новый больной никакого отношения не имеет. Смысл введения в диагностику величины P(D j) состоит в том, что она непостоянна и зависит от географических, сезонных, эпидемиологических и других факторов, которые должны быть учтены при постановке диагноза. Например, в какой-либо больнице наугад было выбрано 100 человек, 70 из них оказались больны гриппом. Значит, вероятность заболевания гриппом у всех пациентов в данной больнице будет равна 70/100=0,7, когда эпидемия гриппа будет ликвидирована, естественно и P(D j) для гриппа в этой больнице будет другой. Величина априорной вероятности диагноза является одной из величин, которая в процессе работы диагностической системы требует мониторинга и текущей коррекции.

Вычисление нормировочного коэффициента (Psc).

Нормировочный коэффициент представляет собой полную вероятность наличия симптомокомплекса при всех заболеваниях. Эта величина несет математический смысл, представляя собой полную сумму попарных произведений условных вероятностей симптомокомплекса для данного диагноза на априорную вероятность этого диагноза:

Psc = P(S сi /D 1) * p(D 1)+ P(S сi /D 2) * p(D 2)+ …+P(S сi /D n) * p(D n)

Полное количество слагаемых в данной сумме равно числу диагнозов, рассматриваемых в данной системе.

5)Вычисление вероятностей диагнозов при данном симптомокомплексе (P(D j /S ci)).

Данный этап являет предпоследним в схеме функционирования системы и основан на использовании теоремы Байеса (формула вероятности гипотез):

P(D j /S ci)=[ P(S сi /D j) x P(D j)] / [ P(Sc) ]

Количество вероятностей диагнозов равно числу диагнозов системы. Иными словами в результате данного этапа работы система вычисляет вероятность каждого из имеющихся диагнозов.

Постановка диагноза.

Этап является наиболее простым и основан на простом сравнении полученных на этапе (5) величин. Наибольшая величина и указывает на тот диагноз, который наиболее вероятен при данном симптомокомплексе. Теоретически возможны случаи, когда вероятность нескольких диагнозов равна. В этом случае необходимо говорить о том, что диагностическая таблица, использующаяся в системе недостаточно совершенна, чтобы “различить” эти диагнозы.

В статистической теории оптимальных приемников, основные понятия которой были рассмотрены в предыдущих параграфах, вопрос об априорных вероятностях полезного сигнала связан с определенными трудностями. Действительно, априорные вероятности нужны для вычисления апостериорных вероятностей, т. е. они необходимы для фактического осуществления оптимального приемника. Однако априорные вероятности часто неизвестны. Так, Вудворд пишет: «Рассмотрим, например, априорную вероятность обнаружения самолета некоторой радиолокационной установкой на расстоянии завтра в утра. Если установка расположена на аэродроме с регулярным движением, статистический анализ прошлого может дать нам нужные вероятности в предположении, что движение самолетов представляет собой стационарный случайный процесс. Для большого класса задач, однако, мы не располагаем статистикой либо потому, что она не изучалась, либо вследствие более фундаментального обстоятельства: в прошлом не существовало совокупности сходных ситуаций, из которой можно было бы вывести определенное суждение».

Как мы показали в § 29, плотности априорных вероятностей можно представить в виде двух множителей

Априорные вероятности. являются соответственно вероятностями наличия и отсутствия полезного сигнала на входе приемника. Эти вероятности наиболее трудно оценить. Априорные вероятностирт являются вероятностями распределения полезных сигналов по неизвестным параметрам при условии, что полезный сигнал присутствует на входе приемника. Эти распределения в ряде случаев можно более или менее уверенно найти из теоретических соображений. Так, например, случайную высокочастотную фазу при некогерентном приеме естественно предположить равномерно распределенной по окружности, амплитуду флюктуирующего сигнала - по закону Релея. Дальность и азимут цели можно в некоторой небольшой области воздушного пространства

предположить равномерно распределенными; при увеличении размеров области это предположение может стать уже несправедливым.

Учитывая выше приведенные рассуждения и предполагая, что закон распределения априорных вероятностей полезного сигнала по неизвестным параметрам известен, мы можем вычислить введенные выше для различных случаев коэффициенты правдоподобия и Если далее образовать отношение апостериорных вероятностей присутствия и отсутствия полезного сигнала, то получим при обнаружении

а при измерении

Эти формулы нетрудно вывести из выражений (29.09), (29.22), (29.28), (29. 33) и соотношений

Формулы (30.02) и (30.03) показывают, что в отношениях апостериорных вероятностей от априорных вероятностей зависит лишь постоянный множитель а принятая функция определяет коэффициенты правдоподобия

Трудность, обусловленную незнанием отношения можно обойти, если изменить определение оптимального приемника и назвать оптимальным приемник, образующий коэффициенты правдоподобия (а не апостериорные вероятности). В таком случае оптимальные приемники по

определению должны выдавать следующие математические величины:

1) при простом обнаружении

2) при сложном обнаружении

3) при простом измерении

4) при сложном измерении

На основании входных данных и образованных с их помощью величин (30.06) обычно приходится принимать решения. Если решать должен человек, например ответить «есть сигнал» или «нет сигнала», то оптимальный приемник лишь помогает человеку, оставляя за ним операцию решения. Надо сказать, что в своих решениях человек всегда использует (часто,не осознавая этого явно) априорные знания о вероятности появления сигнала: в частности, если априорная вероятность появления сигнала достаточно мала, то для ответа «есть сигнал» потребуется более сильное превышение сигнала над шумами, т. е. большее значение

Процесс решения нетрудно автоматизировать. Ограничиваясь задачей обнаружения (сложного или простого), мы должны учесть, что вероятность наличия полезного сигнала

есть монотонная функция коэффициента правдоподобия Совершенно естественно считать, что сигнал присутствует, если вероятность достаточно велика (т. е. достаточно близка к единице), и что полезного сигнала нет, если вероятность достаточно мала. Поэтому простейшее правило решения имеет вид

где некоторое "пороговое" значение вероятности, скажем, ; или

Более сложное правило:

с двумя порогами использует апостериорные вероятности на выходе оптимального приемника более полно, но при этом иногда дает неопределенный ответ. Если сигнал принят, дальнейшая информация в приемник не поступает и на основании имеющихся сведений требуется принять какое-то определенное решение, то единственный выход заключается, очевидно, в применении правила (30.08) с одним порогом. Если же информация поступает в приемник постепенно, то на основании входных данных, накопившихся за фиксированный промежуток времени, можно принять и неопределенное решение, указывающее на необходимость продолжать наблюдение. В этом случае можно применить «двухпороговое» правило (30.09); в принципе можно было бы, вероятно, использовать и более сложные правила.

Рассмотрим более подробно правило (30.08). Коль скоро мы выберем одно из двух возможных решений, то мы всегда можем или принять правильное решение или ошибиться. Ошибки могут быть двух типов. Первый тип ошибки - принятие решения «да», когда на входе присутствует только помеха. Эта ошибка называется ложной тревогой, ее вероятность мы обозначим через Второй тип ошибки - принятие решения «нет», когда на входе присутствуют как помеха, так и полезный сигнал. Эта ошибка называется пропуском сигнала, вероятность этой ошибки мы будем обозначать через Вероятность ложной тревоги является вероятностью принять помеху за сумму сигнал помеха; вероятность пропуска есть вероятностью принять сумму сигнал помеха за чистую помеху.

Правильные решения также могут быть двух типов: правильное обнаружение и правильное необнаружение. Вероятность правильного обнаружения, которую мы обозначим через есть вероятность принять сумму сигнал помеха за сигнал помеха, а вероятность правильного необнаружения, которую мы обозначим через есть вероятность принять помеху за помеху. Очевидно, что условные вероятности: вероятности принять правильное или неправильное решение при условии, что полезного сигнала нет, такие же вероятности при условии, что полезный сигнал присутствует. Поэтому выполняются соотношения

Полцая вероятность принять правильное решение, очевидно, равна

где и суть априорные вероятности отсутствия и наличия сигнала

При использовании правила (30.08) необходимо - задать, помимо порога априорные вероятности Если последние неизвестны, то можно воспользоваться, как это было указано выше, коэффициентом правдоподобия, с помощью которого правило (30.08) перепишется в виде

есть пороговое значение коэффициента правдоподобия. "Двухпороговое" правило (30.09) примет такой вид:

Согласно этим правилам нетрудно построить схемы, автоматически принимающие решения. Таким образом, "решающий" оптимальный ириемник должен образовывать коэффициент правдоподобия и подавать его на вход решающей схемы (30.12) или (30.14). Заметим, что вместо можно использовать любую монотонно возрастающую функцию (например, что часто упрощает схему оптимального приемника. Порог А в формуле (30.12) обычно находят из требования, чтобы вероятность ложных тревог равнялась заданному значению (часто весьма малому, например, или

Остановимся в заключение на терминологии, принятой в литературе.

Наблюдателем Неймана-Пирсона (Neymann-Pearson) называют наблюдателя, который на основании принятых данных принимает решения о наличии сигнала по правилу, которое обеспечивает

максимальную вероятность правильного обнаружения при фиксированной вероятности ложной тревоги за данный промежуток времени наблюдения . В математической статистике доказывается, что наблюдатель Неймана-Пирсона принимает решения как раз по "одно-пороговомуи правилу (30.12), причем величина порога определяется фиксированным значением Любое другое правило решения приводит к меньшим D (при заданных и ).

Идеальный наблюдатель Зигерта (Siegert) принимает решение, обеспечивающее максимальную вероятность по формуле (30.11) при фиксированном времени наблюдения Решение принимается также по правилу (30.12), но величина порога выбирается равной

Последовательный наблюдатель Вальда (Wald) производит анализ данных, непрерывно поступающих на вход приемника. Последовательный наблюдатель имеет возможность задержать решение до поступления новых данных; правило решения для него имеет вид (30.14). Однако математическая теория последовательного наблюдения отличается большей сложностью, и мы в дальнейшем будем исключительно применять схему решения (30.12) с одним порогом, интерпретируя ее в духе наблюдателя Неймана-Пирсона.

Более глубокий подход к статистической теории приема дает современная теория игр и статистических решений, использованная в теории оптимальных приемников Метером и Мидлтоном. Некоторые относящиеся сюда вопросы рассмотрены в приложении

Вопрос № 38. Полная группа событий. Формула полной вероятности. Формулы Байеса.

Двух событий. Независимость в совокупности. Формулировка теоремы умножения в этом случае.

Вопрос № 37. Условная вероятность. Теорема умножения. Определение независимости

Условная вероятность - вероятность одного события при условии, что другое событие уже произошло.

P(А│В)= р(АВ)/ р(В)

Условная вероятность отражает влияние одного события на вероятность другого.

Теорема умножения.

Вероятность произведения событий определяется формулой Р(А 1 ,А 2 ,….А n)= Р(А 1)Р(А 2/ А 1) …Р(А n / А 1 А 2… А n -1)

Для произведения двух событий отсюда следует, что

Р(АВ)=Р(А/В)Р{B)=Р(В/А)Р{А)

Если одно событие не зависит от другого, если появление одного из них не влияет на вероятность появления другого, то последнее также не зависит от первого. Это дает полное основания называть такие события независимыми. Математически независимость означает, что условная вероятность некоторого события совпадает с его вероятностью (безусловной вероятностью).

1.Говорят что событие А не зависит от события В если

P(А│В)=Р(А)

Если событие А не зависит от события В то и событие В не зависит от события А.

2.Если события А и В независимы то Р(АВ)=Р(А)Р(В)-это равенство используется для определения независимых событий.

Следует различать попарную независимость событий и независимость в совокупности.

События А1,А2,….Аn называются независимыми в совокупности если они попарно независимы и каждое из них не зависит от произведения любого набора из остальных событий.

Если события А1,А2,….Аn независимы в совокупности то

Р(А 1 ,А 2 ,….А n)=Р(А 1)Р(А 2)…Р(А n).

В каждой группе какое-либо событие в результате испытания обязательно произойдет, причем появление одного из них исключает появление всех остальных. Такие события называются полной группой событий.

Определение: Если группа событий такова, что в результате испытания обязательно должно произойти хотя бы одно из них, и любые два из них несовместны, то эта группа событий называется полной группой.

Каждое событие из полной группы называется элементарным событием. Каждое элементарное событие - равновозможное, т.к. нет оснований считать, что какое-либо из них более возможное, чем любое другое событие полной группы.

Два противоположных события составляют полную группу.

Относительной частотой события А называется отношение числа опытов, в результате которых произошло событие А к общему числу опытов.

Отличие относительной частоты от вероятности заключается в том, что вероятность вычисляется без непосредственного произведения опытов, а относительная частота – после опыта.

Формула полной вероятности

(где А – некоторое событие, Н1, Н2 … Hi – попарно несовместимы, образубт полную группу, причем А может произойти вместе с H1, H2 Hi)

P(A)=P(A|H 1) P(H 1)+P(A|H 2)P(H 2)+P(A|H 3)P(H 3)+…+P(A|H n)P(H n)

Формула Байеса

Р(Нi |A)=

Замечание. События Нi называют гипотезами вероятности, р(Нi) – априорными вероятностями гипотез Нi, а вероятности Р(Нi/А) – апостериорными вероятностями гипотез Нi

Пусть известен результат опыта, а именно то, что произошло событие А. Этот факт может изменить априорные (то есть известные до опыта) вероятности гипотез. Для переоценки вероятностей гипотез при известном результате опыта используется формула Байеса:

Пример. После двух выстрелов двух стрелков, вероятности попаданий которых равны 0,6 и 0,7, в мишени оказалась одна пробоина. Найти вероятность того, что попал первый стрелок.

Решение. Пусть событие А – одно попадание при двух выстрелах,

а гипотезы: Н1 – первый попал, а второй промахнулся,

Н2 – первый промахнулся, а второй попал,

Н3 – оба попали,

Н4 – оба промахнулись.

Вероятности гипотез:

р(Н1) = 0,6·0,3 = 0,18,

р(Н2) = 0,4·0,7 = 0,28,

р(Н3) = 0,6·0,7 = 0,42,

р(Н4) = 0,4·0,3 = 0,12.

Тогда р(А/Н1) = р(А/Н2) = 1,

р(А/Н3) = р(А/Н4) = 0.

Следовательно, полная вероятность р(А) = 0,18·1 + 0,28·1 + 0,42·0 + 0,12·0 = 0,46.

Формула полной вероятности позволяет вычислить вероятность интересующего события через условные вероятности этого события в предположении неких гипотез, а также вероятностей этих гипотез.

Определение 3.1. Пусть событие А может произойти только совместно с одним из событий Н1, Н2,…, Нп, образующих полную группу несовместных событий. Тогда события Н1, Н2,…, Нп называются гипотезами.

Теорема 3.1. Вероятность события А, наступающего совместно с гипотезами Н1, Н2,…, Нп, равна:

где p(Hi) – вероятность i- й гипотезы, а p(A/Hi) – вероятность события А при условии реализации этой гипотезы. Формула (P(A)= ) носит название формулы полной вероятности

Вопрос № 39. Схема Бернулли. Вероятность m успехов в серии из n испытаний

Игнорирование априорной вероятности (base rate neglect), или как ее еще называют, ошибка априорной вероятности (base rate fallacy) - это когнитивное искажение (cognitive bias), приводящее к ошибкам в оценке вероятности, в частности, вероятности того, является ли человек носителем того или иного свойства или относится ли он к той или иной категории.

Нужно сказать, что английские слова «base rate» обозначают не априорную вероятность, а распространенность явления, качества (например, заболевания), в генеральной совокупности. Априорная же вероятность обозначается в английском языке термином «prior probability». Но в случае рассматриваемого когнитивного искажения понятия «base rate» и «prior probability» синонимичны.

А теперь давайте сразу перейдем к конкретике, решив следующую задачу.

В племени Мумба-Юмба 1% его членов имеют редкую наследственную болезнь, назовем ее «белемнит».

У Вас есть прибор, который в 80% случаев обнаруживает белемнит у больного, но в 10% случаев обнаруживает белемнит у здорового.

Вы обследовали человека, и прибор показал, что у него белемнит.

Какова вероятность того, что у этого человека на самом деле белемнит.

Если Вы ответили 80%, то это не удивительно: большинство участников экспериментов на игнорирование априорной вероятности отвечают также. Причем такая ситуация наблюдается не только в экспериментах, но и в реальной жизни, в частности, у реальных практикующих врачей.

Но дело в том, что ответ 80% - неверный, он как раз и демонстрирует игнорирование априорной вероятности. Так что давайте разбираться.

Допустим, в племени белемнитов всего 1000 человек. Получается, что больных белемнитом - 10 человек (1% от 1000). Из этих 10 прибор обнаружит белемнит у 8 человек (80% от 10). Но проблема в том, что он обнаружит белемнит и у здоровых людей, т.е. у 10% из 990. Но 10% от 990 - это 99 человек. Получается, что из 107 человек (99+8), которым прибор поставил диагноз «белемнит», эта болезнь реально есть только у 8. Это означает, что вероятность того, что у Вашего подопытного, действительно, белемнит, составляет 8/107*100% = 7,47%. Это намного меньше, чем 80%, правда же?

(Приведенное решение является упрощенным и иллюстративным).

Рассмотрим эту же ситуацию с помощью кругов Эйлера (диаграмм Венна).

На рисунке большая окружность - это все племя Мумба-Юмба, а маленькая окружность - это члены племени, больные белемнитом.

А теперь мы проводим еще одну окружность, показывающую, какой части членов племени прибор поставил диагноз «белемнит».

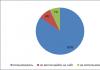
Давайте рассмотрим детальнее получившиеся области, выделив их разными цветами.

• зеленая область - это больные, у которых болезнь есть, и она выявлена;
• фиолетовая область - это больные, у которых болезнь есть, но не выявлена (ложноотрицательный ответ);
• красная область - это здоровые люди, у которых болезнь выявлена ошибочно (ложноположительный ответ).

Этот пример не просто выдуман, он отражает реальную ситуацию с медицинскими диагнозами. Например, при использовании маммографии врачи игнорируют априорную вероятность рака груди у женщин и ориентируются только на показатели маммографа. На самом деле, таких примеров множество, а игнорирование априорной вероятности присуще врачам не в меньшей степени, чем всем людям.

Необходимо подчеркнуть, что игнорирование априорной вероятности наблюдается не только в ситуациях приборной диагностики. Так, например, на мой взгляд, многие случаи обнаружения человеком у себя редких и экзотических болезней объясняются игнорированием априорной вероятности: человек читает описания симптомов, находит их у себя, но не учитывает, что болезнь слишком редка, чтобы ей заболеть.

Со мной произошел подобный случай, когда я был подростком. Тогда я прочитал какую-то народную медицинскую энциклопедию и по симптомам обнаружил у себя трахому (мне показалось, что мои ресницы растут неровно, выпадают, кроме того на склере одного из глаз у меня было некое новообразование). Лекарством от трахомы, которое описывалось в этой энциклопедии, было промывание глаз лимонным соком. К счастью, я успел покапать в глаза лимонный сок (это, кстати, очень неприятная процедура!) всего несколько раз до того, как на приеме окулиста услышал ключевую вещь: трахома на территории РФ давно побеждена (еще в советское время), т.е. априорная вероятность заболеть трахомой составляет 0%.

(Отдельное спасибо издателям, распространяющим книги о здоровье с глубоко устаревшей информацией…).

Игнорирование априорной вероятности проявляется, конечно, не только в связи с вопросами медицины и здоровья. Так, наши суждения о людях тоже оказываются неверными из-за игнорирования априорной вероятности. Например, для бабушек, сидящих у подъезда, любая накрашенная девушка в короткой юбке относится к категории девушек легкого поведения. Можно предположить, что суждения бабушек неверны, поскольку по-настоящему легким является поведение только подавляющего меньшинства девушек (мы можем обоснованно это предположить, хотя бы исходя из того, что накраситься и надеть короткую юбку гораздо проще, чем на самом деле вести себя легко).

Поэтому прежде чем относить человека к той или иной категории или приписывать ему то или иное качество, нужно выяснить, насколько широко распространена эта категория и насколько часто встречается это качество.

Конечно, часто проблема состоит в том, что мы не обладаем достоверной информацией об априорной вероятности. Но это, как говориться, уже совсем другая история…

И в заключение хочу отметить, что внимательный читатель должен был обнаружить определенную связь между таким когнитивным искажением как игнорирование априорной вероятности и таким искажением как ошибка конъюнкции (cunjunction fallacy). И это не удивительно: оба этих искажения порождаются эвристикой репрезентативности и даже относятся к одной и той же категории когнитивных искажений - к так называемому игнорированию распространенности (extension neglect).

Думай медленно… решай быстро / Даниэль Канеман. - Москва: АСТ, 2014. - 653 с.